Résumé du conte

Une petite poule rousse demande de l'aide dans la basse-cour pour planter, récolter, moudre et pétrir le blé, mais personne ne veut l'aider. Elle finit par manger seule le pain qu'elle a fait !

À propos du conte

Une histoire simple, cumulative, rythmée, parfaite pour une première narration !

Son schéma très simple se prête parfaitement à la transmission orale. Elle peut aussi se chanter.

Cette histoire est idéale pour conter pour la première fois à de jeunes enfants, car tout le monde peut la raconter en chœur, et il y a quelques rôles à mimer pour ceux qui se sentent à l'aise.

Identifier et représenter les étapes clés du conte pour mieux le mémoriser :

👉 Découvrir le conte

Maths

Ordre, conditions, logique…
et une poule qui fait tout

👦🏻 Âge cible :  5-6 ans

⏰ Durée : à adapter selon le projet

🎯 Objectifs pédagogiques

Se familiariser avec l’idée qu’un raisonnement mathématique se construit selon des étapes ordonnées et explicitées.

D’un point de vue mathématique, il y a dans cette histoire un ordonnancement logique : les étapes doivent être réalisées dans un certain ordre, et chacune est nécessaire à l’aboutissement du processus.

• Pour la poule :

La poule doit réaliser toutes les étapes, sans en oublier aucune, afin de réaliser le gâteau.

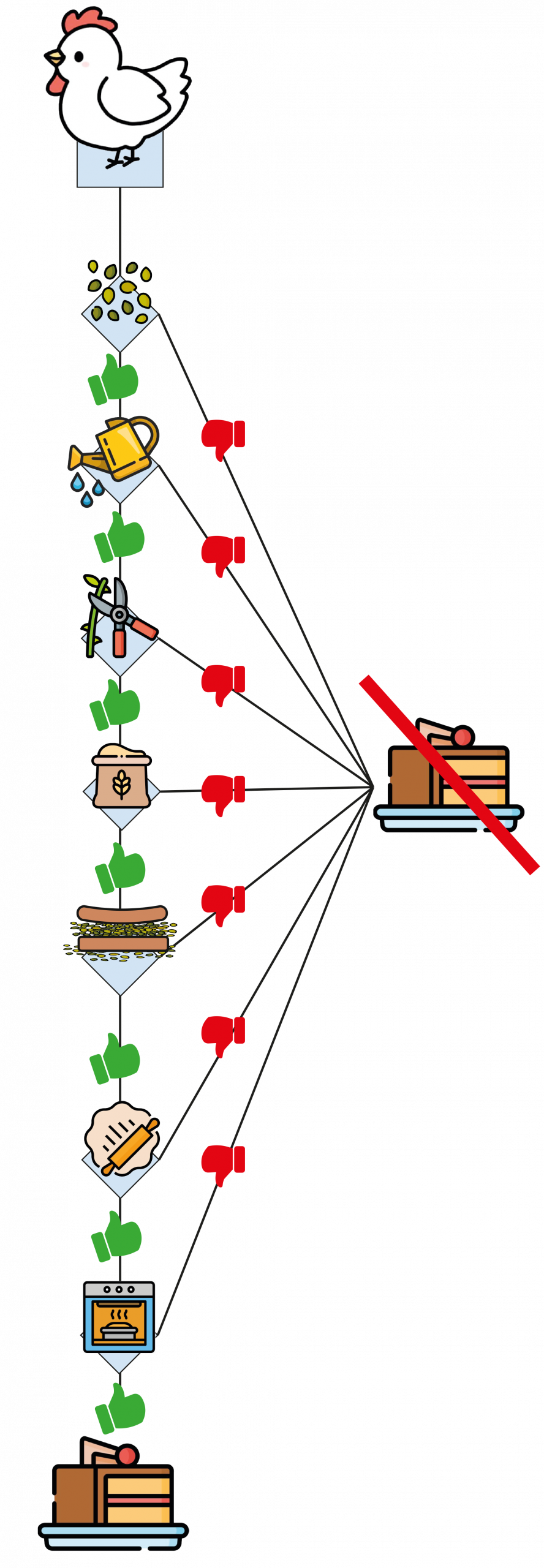
• Pour les autres animaux :

On peut imaginer qu’aider une seule fois leur donnerait le droit de manger une part du gâteau et c’est lorsqu’ils n’aident jamais qu’ils finissent par ne pas y avoir droit.

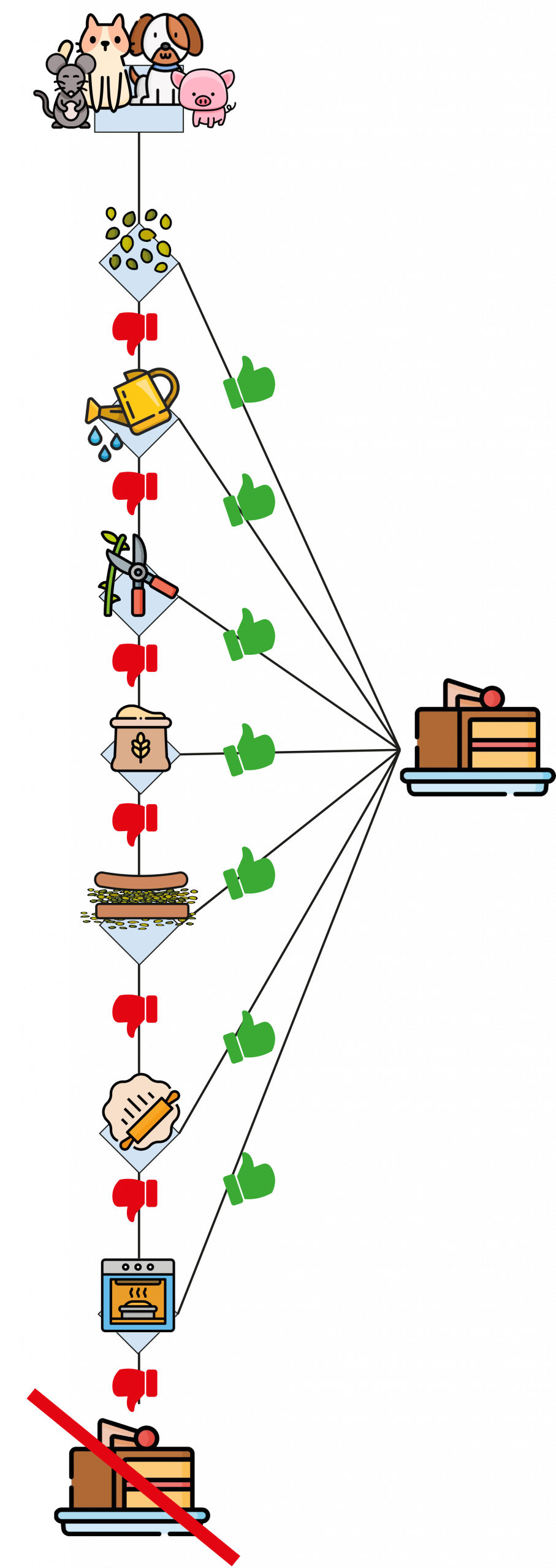
D’un point de vue mathématique, cette situation illustre un principe logique bien connu :

👉 Si le cochon avait aidé à arroser (par exemple), il aurait eu une part de gâteau.

La négation d’une proposition contenant des “OU” correspond à un “ET” entre les négations des conditions :

• Si, pour manger du gâteau, il suffit :

d’aider à planter, OU à arroser, OU à moissonner, OU à transporter, OU à moudre, OU à pétrir, OU à faire cuire…

 

• Alors,  à l’inverse :

Puisque le chat n’a jamais aidé, alors il n’a pas de gâteau.

si on n’aide pas à planter, ET qu’on n’aide pas à arroser, ET qu’on n’aide pas à moissonner, ET qu’on n’aide pas à transporter, ET qu’on n’aide pas à moudre ET qu’on n’aide pas à pétrir ET qu’on n’aide pas à faire cuire

→ a pour conséquence que l’on ne mange pas de gâteau.

 

👉 En logique, si on nie une phrase du type : “A ou B ou C”,

alors cela revient à dire : “pas A ET pas B ET pas C”.

 

 

🟢 Activités

• Reprendre le conte en modulant les réponses des animaux&nbsp: par exemple, le cochon veut bien aider à semer le grain de blé, réponses négatives des autres ; le chat aide à la deuxième étape, la souris n’aide jamais. Arrêter le récit avant le partage du gâteau : “À qui peut-on donner du gâteau ?”

• Reprendre le conte “l’année d’après” en ayant quelques animaux qui coopèrent (ils ont mûri) et donc ont une part de gâteau à la fin: favorise l’écoute active de l’histoire et la constitution de la collection des animaux coopératifs (qui auront une part?). Laisser les enfants proposer un traitement des animaux: “le chat, non, il n’a rien fait, il n’aura rien” ou bien “ils n’ont pas tous aidés tout le temps, personne n’aura rien” ou au contraire “tout le monde a une part même s’ils n’ont rien fait”, pour discuter autour de la justice et finalement de la logique, pour établir la condition “il suffit d’avoir aidé une fois pour avoir une part” et la conséquence équivalente: “si tu n’as aidé aucune fois, tu n’as pas de part de gâteau”.

• Ordonnancement: Illustrer les étapes par des pictogrammes chacun affectée à un enfant et les laisser s’ordonner.

🟢 Autres activités

Décliner avec d’autres projets, où les différentes étapes devraient être ordonnées par les enfants (voire même explicitées par les enfants) :

• Ordonnancer les étapes de confection d’une couverture :

Élever le mouton, le tondre, laver la laine,  la filer, tricoter la couverture → se blottir dessous !

• Ordonnancer les étapes de l’habillement :  

Certaines étapes sont ordonnées, (enfiler un pantalon avant des chaussures), mais d'autres ne le sont pas, (mettre une chemise avant ou après une culotte).

• Inventer un autre projet :

Créer une recette, préparer un goûter, construire une cabane… Les élèves peuvent ordonner les étapes et même les expliquer.

✅ Conclusion pédagogique

Ces activités permettent aux élèves de comprendre que toute action construite repose toujours sur un enchaînement structuré.

Ordonner des gestes, c’est déjà raisonner : c’est ce qu’on attend dans un raisonnement mathématique où toutes les étapes du raisonnement sont ordonnées et doivent être explicitées.