Story Summary

A little red hen asks for help in the farmyard to plant, harvest, grind, and knead the wheat, but no one wants to help her. In the end, she eats the bread she made all by herself!

About the Story

A simple, cumulative, rhythmic story — perfect for a first narration!

Its very simple structure is perfectly suited for oral storytelling. It can even be sung.

This story is ideal for telling young children for the first time, as everyone can recite it together, and there are some roles to mime for those who feel comfortable.

Identify and represent the key stages of the story to better memorize it:

👉 Discover the story

Maths

Order, conditions, logic…
and a hen who does it all

👦🏻 Target Age: 5–6 years

⏰ Duration: to be adapted depending on the project

🎯 Learning Objectives

Become familiar with the idea that mathematical reasoning is built through ordered and explicit steps.

From a mathematical point of view, this story contains a logical ordering: the steps must be carried out in a certain order, and each one is necessary for the process to succeed.

• For the hen:

The hen must complete all the steps, without skipping any, in order to make the cake.

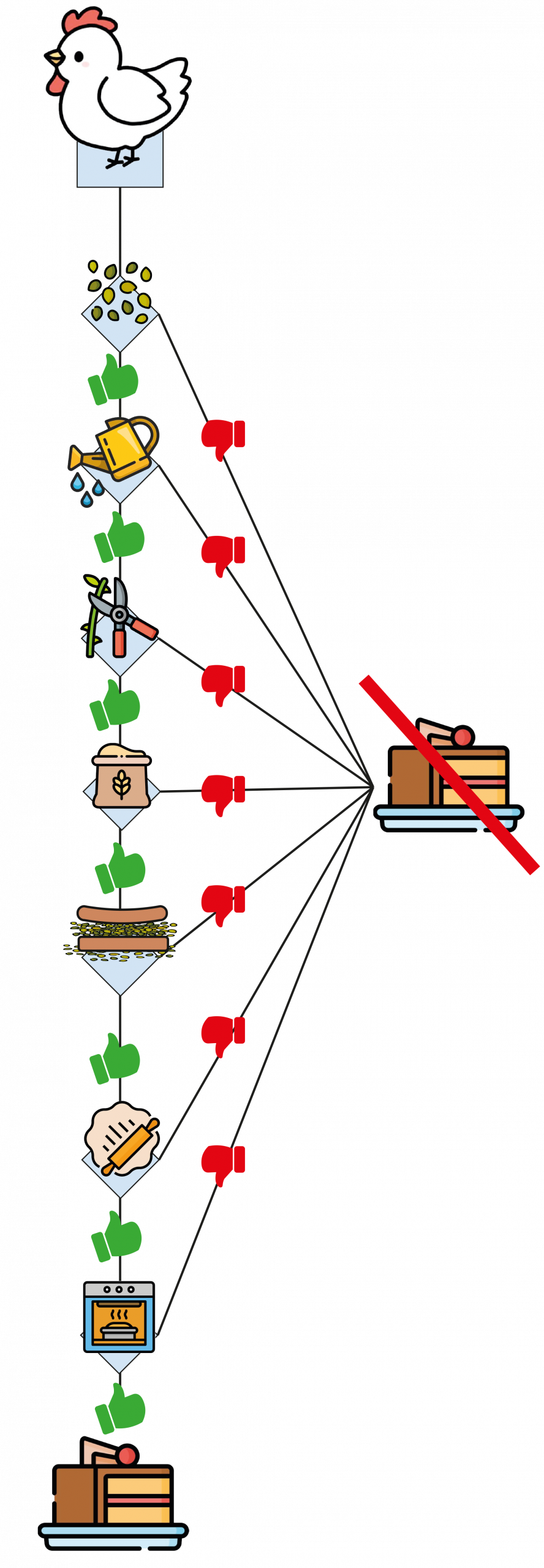
• For the other animals:

We can imagine that helping even once would give them the right to eat a slice of the cake, and it is only when they never help that they end up with none.

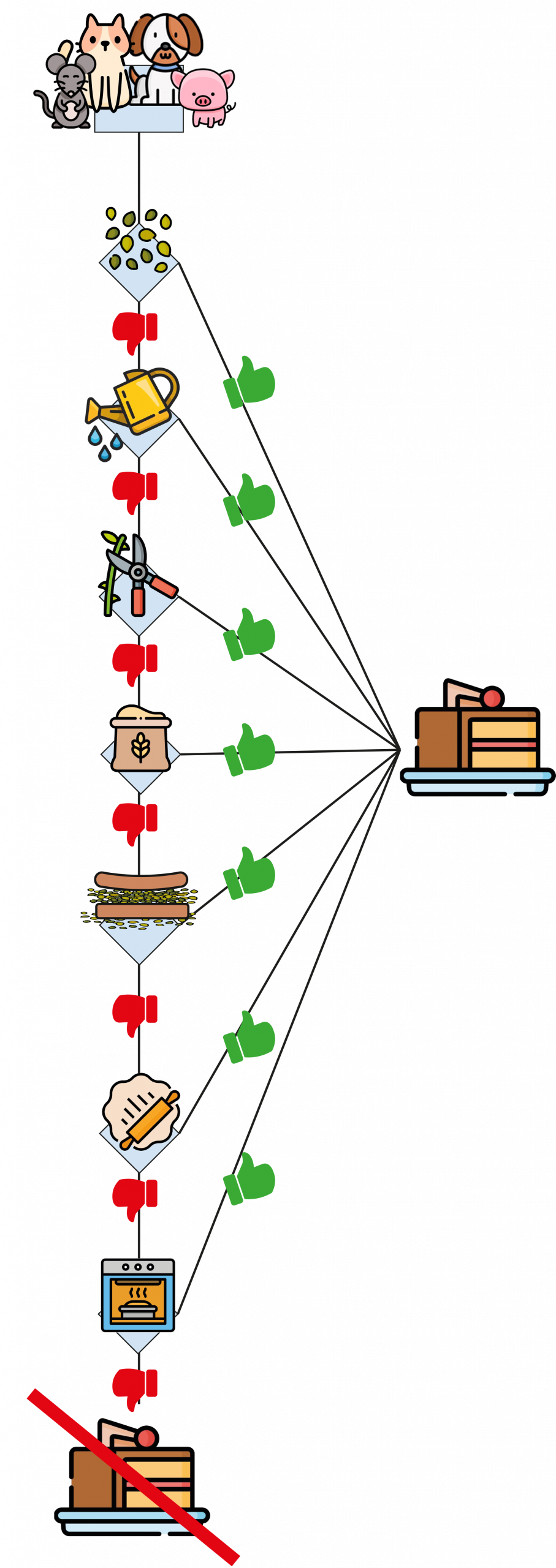
From a mathematical point of view, this situation illustrates a well-known logical principle:

👉 If the pig had helped with watering (for example), he would have had a piece of cake.

The negation of a proposition containing “OR” corresponds to an “AND” between the negations of the conditions:

• If, to eat cake, it is enough to:

help plant, OR water, OR harvest, OR carry, OR grind, OR knead, OR bake…

• Then, conversely:

Since the cat never helped, then he has no cake.

If you do not help with planting, AND do not help with watering, AND do not help with harvesting, AND do not help with carrying, AND do not help with grinding, AND do not help with kneading, AND do not help with baking,

→ then you do not eat cake.

👉 In logic, if you negate a sentence of the type: “A or B or C”,

then it amounts to saying: “not A AND not B AND not C”.

🟢 Activities

• Retell the story while changing the animals’ answers: for example, the pig agrees to help sow the grain of wheat, the others refuse; the cat helps at the second stage, the mouse never helps. Stop the story before sharing the cake: “Who can be given cake?”

• Retell the story “the following year” with some animals cooperating (they have matured) and therefore receiving a share of the cake at the end: this fosters active listening to the story and building the collection of cooperative animals (who will get a share?). Let the children propose how to treat the animals: “the cat, no, he did nothing, he gets nothing,” or “they didn’t all help all the time, no one gets anything,” or on the contrary “everyone gets a piece even if they didn’t do anything,” in order to discuss fairness and ultimately logic, to establish the condition “helping even once is enough to get a piece” and the equivalent consequence: “if you never helped, you don’t get cake.”

• Ordering: Illustrate the steps with pictograms, each assigned to a child, and let them arrange themselves in order.

🟢 Other Activities

Apply to other projects, where the different steps must be ordered by the children (and even explicitly stated by them):

• Order the steps of making a blanket:

Raise the sheep, shear it, wash the wool, spin it, knit the blanket → snuggle underneath!

• Order the steps of getting dressed:

Some steps are ordered (put on trousers before shoes), but others are not (shirt before or after underwear).

• Invent another project:

Create a recipe, prepare a snack, build a hut… The students can order the steps and even explain them.

✅ Pedagogical Conclusion