Resumen del cuento

Una pequeña gallinita roja pide ayuda en el corral para plantar, cosechar, moler y amasar el trigo, pero nadie quiere ayudarla. ¡Al final se come sola el pan que ha hecho!

Acerca del cuento

Una historia sencilla, acumulativa y rítmica, ¡perfecta para una primera narración!

Su esquema muy simple se presta perfectamente a la transmisión oral. También puede cantarse.

Este cuento es ideal para contar por primera vez a niños pequeños, porque todo el mundo puede relatarlo al unísono, y hay algunos papeles que se pueden mimar para quienes se sientan cómodos.

Identificar y representar las etapas clave del cuento para memorizarlo mejor:

👉 Descubrir el cuento

Maths

Orden, condiciones, lógica…
y una gallina que lo hace todo

👦🏻 Edad objetivo: 5–6 años

⏰ Duración: a adaptar según el proyecto

🎯 Objetivos pedagógicos

Familiarizarse con la idea de que un razonamiento matemático se construye según etapas ordenadas y explicitadas.

Desde el punto de vista matemático, en esta historia hay un ordenamiento lógico: las etapas deben realizarse en cierto orden, y cada una es necesaria para culminar el proceso.

• Para la gallina:

La gallina debe realizar todas las etapas, sin olvidar ninguna, para poder hacer el pastel.

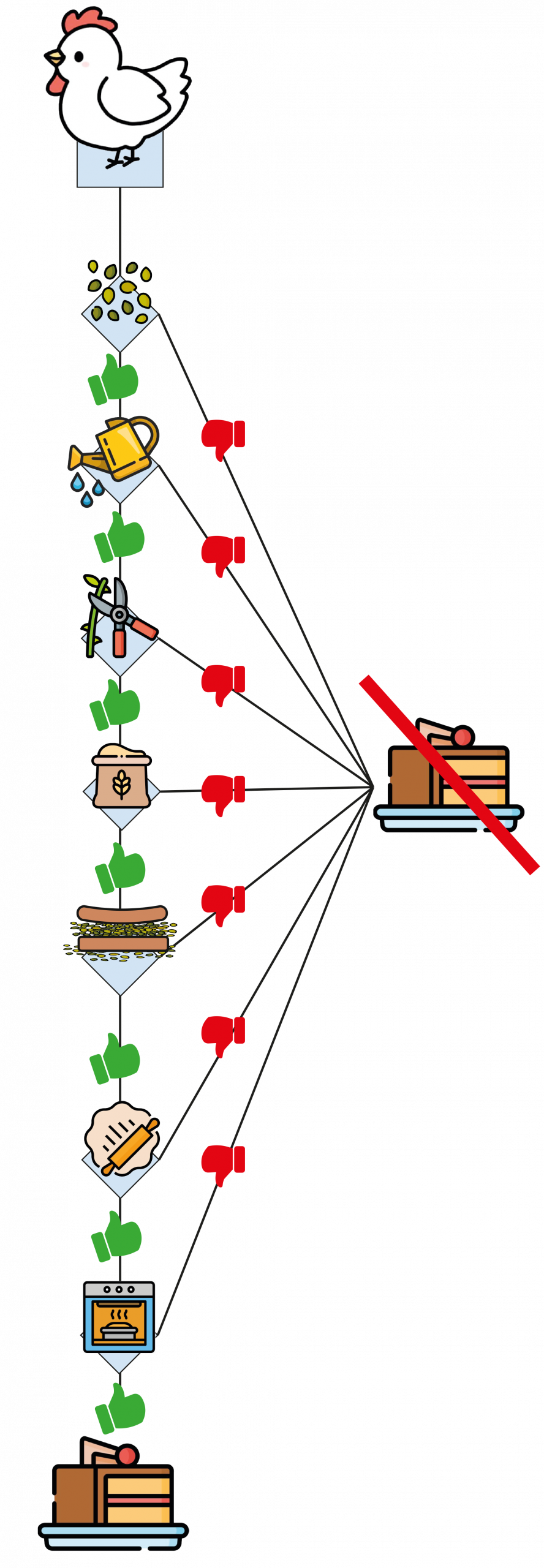
• Para los otros animales:

Podemos imaginar que ayudar una sola vez les daría derecho a comer una porción de pastel, y que es cuando no ayudan nunca cuando terminan por no tener derecho.

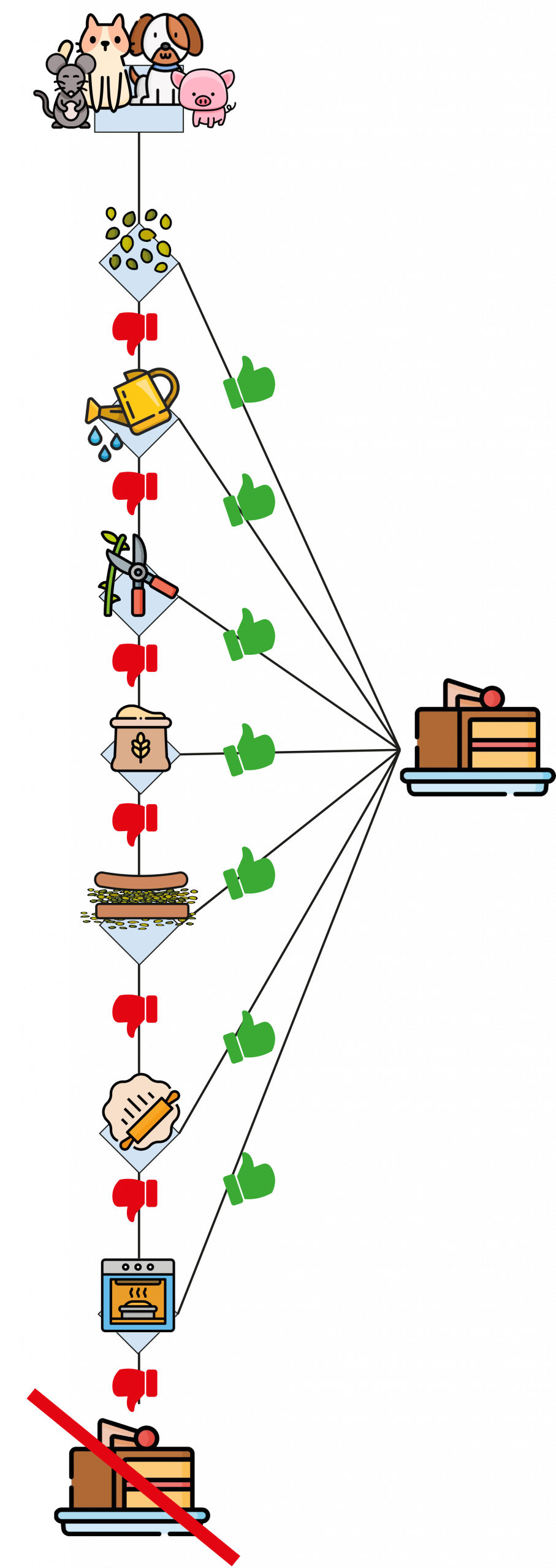
Desde un punto de vista matemático, esta situación ilustra un principio lógico bien conocido:

👉 Si el cerdo hubiera ayudado a regar (por ejemplo), habría tenido una porción de pastel.

La negación de una proposición que contiene “O” corresponde a una “Y” entre las negaciones de las condiciones:

• Si, para comer pastel, basta con:

ayudar a plantar, O a regar, O a segar, O a transportar, O a moler, O a amasar, O a hornear…

• Entonces, a la inversa:

Puesto que el gato no ayudó nunca, no tiene pastel.

si no se ayuda a plantar, Y no se ayuda a regar, Y no se ayuda a segar, Y no se ayuda a transportar, Y no se ayuda a moler Y no se ayuda a amasar Y no se ayuda a hornear

→ tiene como consecuencia que no se come pastel.

👉 En lógica, si negamos una frase del tipo: “A o B o C”,

entonces equivale a decir: “no A Y no B Y no C”.

🟢 Actividades

• Retomar el cuento modulando las respuestas de los animales: por ejemplo, el cerdo acepta ayudar a sembrar el grano de trigo, respuestas negativas de los demás; el gato ayuda en la segunda etapa; el ratón no ayuda nunca. Detener el relato antes de repartir el pastel: “¿A quién se le puede dar pastel?”

• Retomar el cuento “al año siguiente” con algunos animales que cooperan (han madurado) y por tanto tienen una porción de pastel al final: favorece la escucha activa de la historia y la formación de la colección de animales cooperativos (¿quiénes tendrán porción?). Dejar que los niños propongan un trato para los animales: “el gato, no, no ha hecho nada, no tendrá nada” o bien “no han ayudado todos todo el tiempo, nadie tendrá nada” o, por el contrario, “todo el mundo tiene una porción aunque no hayan hecho nada”, para debatir sobre la justicia y, finalmente, sobre la lógica, y así establecer la condición “basta con haber ayudado una vez para tener una porción” y la consecuencia equivalente: “si no has ayudado ninguna vez, no tienes porción de pastel”.

• Ordenación: ilustrar las etapas con pictogramas, cada uno asignado a un niño, y dejar que se coloquen en orden.

🟢 Otras actividades

Declinar con otros proyectos, donde las diferentes etapas deban ser ordenadas por los niños (e incluso explicitadas por ellos):

• Ordenar las etapas de confección de una manta:

Criar la oveja, esquilarla, lavar la lana, hilarla, tejer la manta → ¡acurrucarse debajo!

• Ordenar las etapas de vestirse:

Algunas etapas están ordenadas (ponerse un pantalón antes que los zapatos), pero otras no (ponerse una camisa antes o después de la ropa interior).

• Inventar otro proyecto:

Crear una receta, preparar una merienda, construir una cabaña… El alumnado puede ordenar las etapas e incluso explicarlas.

✅ Conclusión pedagógica