Une boîte a une forme et une contenance. Le mythe commence par la mise en sarcophage d’Horus. Certains candidats sont trop grands, d’autres trop larges, d’autres trop petits. Seul Horus entre parfaitement dans cette boîte qui a été construite exprès pour le piéger. Voici des boîtes. Comment les classer? Et en terme de contenance?

Tout d’abord, il y aura des cas simples: une boîte rentre complètement dans l’autre. Puis il y en aura des plus complexes: une boîte assez fine, rentrera dans une plus large, mais dépassera en hauteur. Il est courant que les élèves se concentrent sur une seule dimension pour décider et classent comme plus volumineuse la boîte la plus longue. Il faudra lever l'ambiguïté en remplissant l’une de semoule et en la déversant dans l’autre. Si tout rentre, c’est la seconde qui est la plus grande, si ça déborde, c’est la première.

À l’aide d’une calculatrice, calculer $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64}$

Comparer à $1 - \frac{1}{64}$

Sur une bande de papier, qu’on prendra comme l’unité, marquer en pliant la moitié, puis le quart, le huitième, le seizième… Comprendre visuellement qu’à chaque étape, on a l’unité qui est décomposée en :

$1 = \frac{1}{2} + \frac{1}{2} = \frac{1}{2} + \frac{1}{4} + \frac{1}{4} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{8} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{16} = \frac{1}{2} + \frac{1}{4} +$ $\frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{32} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{64}$

Découper la bande unité :

Puis mesurez chaque bande proposée en n’utilisant que ces petites bandelettes et écrivez ce que vous obtenez.

Vous aurez préparé des bandes de feuilles A4 verticales et des fractions simples de celles-ci : faire constater que :

$\frac{3}{4} = \frac{1}{2} + \frac{1}{4} \quad$,$\quad\frac{5}{8} = \frac{1}{2} + \frac{1}{8}\quad$,$\quad\frac{3}{8} = \frac{1}{4} + \frac{1}{8}\quad$,$\quad\frac{1}{3} = \frac{1}{4} + \frac{1}{16} + \frac{1}{64} + \cdots\quad$,$\quad\frac{2}{3} = \frac{1}{2} + \frac{1}{8} + \frac{1}{32} + \cdots$

Pour ces derniers, deux constructions, à base d’un carré ou d’un triangle équilatéral, définissant par les milieux quatre petites formes semblables, et recommencer à l’intérieur. La surface totale est décomposée en trois tiers, un rouge, un bleu, un vert, qui eux-mêmes sont composés du quart, du seizième, du soixante-quatrième etc. Occasion à de belles constructions et le frisson de frôler l’infini.

Une autre version du paradoxe est celui de Zénon d’Élée qui voulait montrer que rien ne change dans ce monde : Achille, le héros grec le plus rapide, ne rattrapera jamais la tortue, en effet, il faudra d’abord qu’il atteigne l’endroit où était la tortue au départ. Mais pendant ce temps, la tortue aura avancé un peu, et le même raisonnement s’appliquera. De même, la flèche (ou le coureur) n’atteindra jamais sa cible, car pour l’atteindre, il faudra qu’elle fasse la moitié du chemin. Une fois-là, il lui restera le moitié de la moitié, soit le quart, puis le huitième, le seizième, le trente-deuxième, le soixante-quatrième, le cent-vingt-huitième etc… À chaque fois, il lui restera une distance à parcourir.

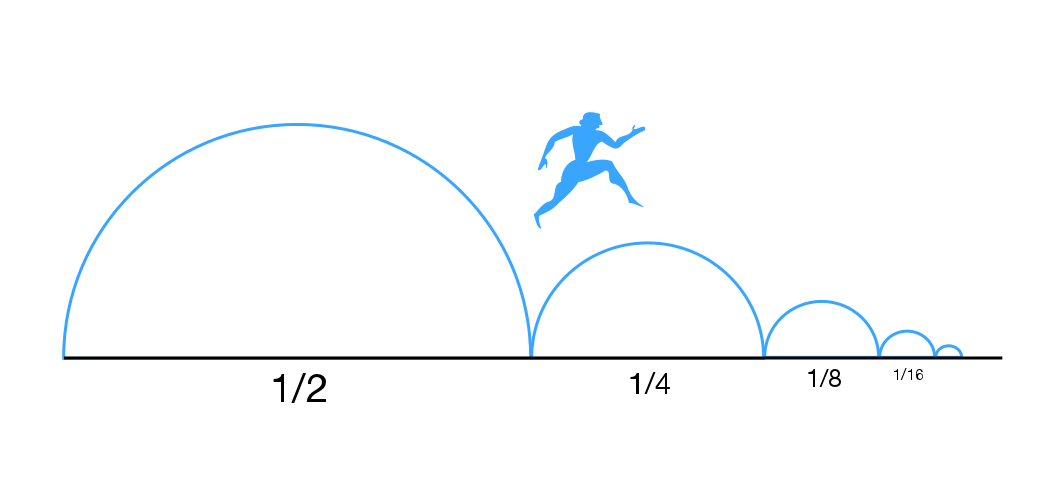
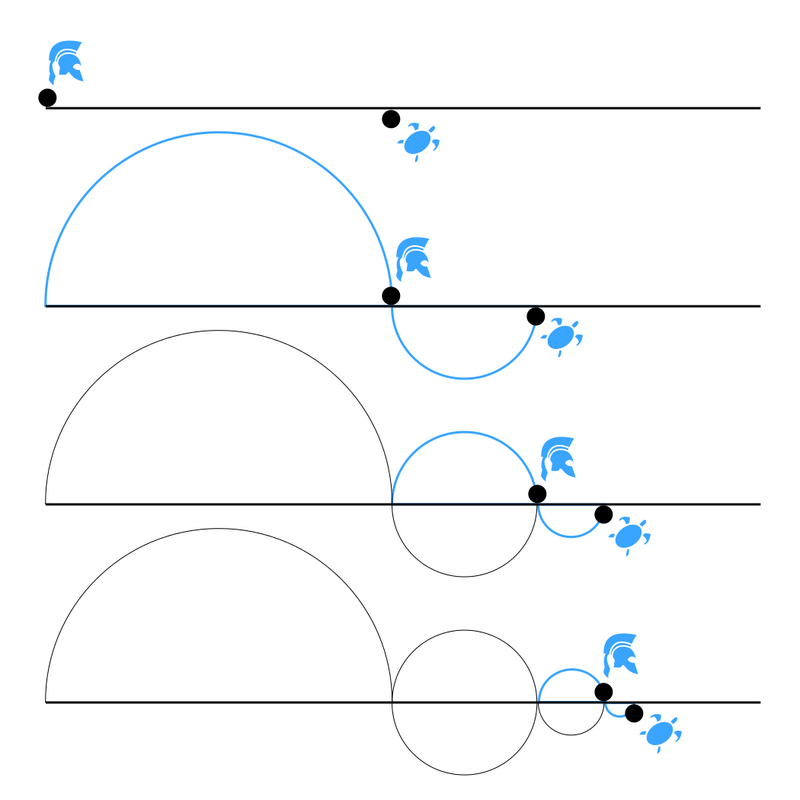
À l’aide d’une calculatrice, calculer

$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64}$

Comparer à $1 - \frac{1}{64}$ 

Et si jamais on ne s’arrêtait pas

$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{128} + \frac{1}{256} + \frac{1}{512} + \cdots$

Et si on n’avait pas coupé en deux mais en 10 ? Que vaut

$\frac{1}{10} + \frac{1}{100} + \frac{1}{1000} + \frac{1}{10000} + \frac{1}{100000} + \cdots$

Comparer à $\frac{1}{9}$ 

Alors que vaut $\frac{9}{9} = \,?$  Et finalement que vaut

$\frac{9}{10} + \frac{9}{100} + \frac{9}{1000} + \frac{9}{10000} + \frac{9}{100000} + \cdots = 0,99999\ldots$

La notion de limite n’est maîtrisée que très récemment par les mathématiciens, au milieu du XIXe siècle, aussi, il ne faut pas s’étonner d’avoir des approches très contrastées : accepter comme évident et allant de soi que le mouvement est possible, que la flèche atteindra bien sa cible d’un côté et de l’autre, refuser que $0,999\ldots = 1$

ce qui pourtant, d’un point de vue logique est rigoureusement la même chose. En effet on accepte que

$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{128} + \frac{1}{256} + \frac{1}{512} + \cdots = 1$

 ce qui s’écrit en base deux

$1 = 0,11111\ldots_b$

mais en base dix (la base usuelle), si

$0,11111\ldots = \frac{1}{9}$

 ne pose pas de problème, tout comme

$0,33333\ldots = \frac{3}{9} = \frac{1}{3}$

l’écriture

$0,99999\ldots = \frac{9}{9} = 1$

n’est pas acceptée par les élèves. C’est pourtant une égalité mathématique (qui n’est exigible qu’en première, après avoir vu les suites géométriques et leurs sommes).