Una caja tiene una forma y una capacidad. El mito comienza con el encierro en un sarcófago. Algunos candidatos son demasiado largos, otros demasiado anchos, otros demasiado pequeños. Solo uno encaja a la perfección en la caja hecha expresamente para atraparlo. He aquí varias cajas. ¿Cómo clasificarlas? ¿Y en términos de capacidad?

Al principio habrá casos sencillos: una caja cabe por completo dentro de otra. Luego, otros más complejos: una caja estrecha cabrá en otra más ancha, pero sobresaldrá en altura. Es frecuente que el alumnado se centre en una única dimensión para decidir y clasifique como más voluminoso el recipiente más largo. Habrá que despejar la ambigüedad llenando una con sémola y vertiéndola en la otra. Si todo cabe, la segunda es mayor; si se derrama, la primera lo es.

Con ayuda de una calculadora, calcular $\\frac{1}{2} + \\frac{1}{4} + \\frac{1}{8} + \\frac{1}{16} + \\frac{1}{32} + \\frac{1}{64}$

 

Comparar con $1 - \\frac{1}{64}$

En una tira de papel que tomaremos como la unidad, marcar doblando la mitad, luego el cuarto, el octavo, el dieciseisavo… Comprender visualmente que en cada etapa, la unidad se descompone en:

$1 = \\frac{1}{2} + \\frac{1}{2} = \\frac{1}{2} + \\frac{1}{4} + \\frac{1}{4} = \\frac{1}{2} + \\frac{1}{4} + \\frac{1}{8} + \\frac{1}{8} = \\frac{1}{2} + \\frac{1}{4} + \\frac{1}{8} + \\frac{1}{16} + \\frac{1}{16} = \\frac{1}{2} + \\frac{1}{4} + \\frac{1}{8} + \\frac{1}{16} + \\frac{1}{32} + \\frac{1}{32} = \\frac{1}{2} + \\frac{1}{4} + \\frac{1}{8} + \\frac{1}{16} + \\frac{1}{32} + \\frac{1}{64} + \\frac{1}{64}$

Recortar la tira unidad:

Luego medir cada tira propuesta utilizando solo estas tiras pequeñas y escribir lo obtenido.

Habréis preparado tiras de hojas A4 en vertical y fracciones simples de las mismas: hacer constar que:

$\\frac{3}{4} = \\frac{1}{2} + \\frac{1}{4} \\,,$ $\\quad\\frac{5}{8} = \\frac{1}{2} + \\frac{1}{8}\\quad$, $\\quad\\frac{3}{8} = \\frac{1}{4} + \\frac{1}{8}\\quad$, $\\quad\\frac{1}{3} = \\frac{1}{4} + \\frac{1}{16} + \\frac{1}{64} + \\cdots\\quad$, $\\quad\\frac{2}{3} = \\frac{1}{2} + \\frac{1}{8} + \\frac{1}{32} + \\cdots$

Para estos últimos, dos construcciones —a partir de un cuadrado o de un triángulo equilátero— definiendo por los puntos medios cuatro pequeñas formas semejantes, y repetir en el interior. La superficie total se descompone en tres tercios, uno rojo, uno azul y uno verde, que a su vez se componen del cuarto, del dieciseisavo, del sesentaicuatroavo, etc. Ocasión para bellas construcciones y el cosquilleo de rozar el infinito.

Otra versión del paradoxo es la de Zenón de Elea, que quería mostrar que nada cambia en este mundo: Aquiles, el héroe griego más rápido, nunca alcanzará a la tortuga; en efecto, primero deberá llegar al lugar donde estaba la tortuga al inicio. Pero mientras tanto, la tortuga habrá avanzado un poco, y el mismo razonamiento se aplicará de nuevo. Del mismo modo, la flecha (o el corredor) nunca alcanzará su objetivo, porque para hacerlo deberá recorrer primero la mitad del camino. Una vez allí, le quedará la mitad de la mitad, es decir, el cuarto, luego el octavo, el dieciseisavo, el treintaydosavo, el sesentaicuatroavo, el ciento veintioctavo, etc. Cada vez le quedará una distancia por recorrer.

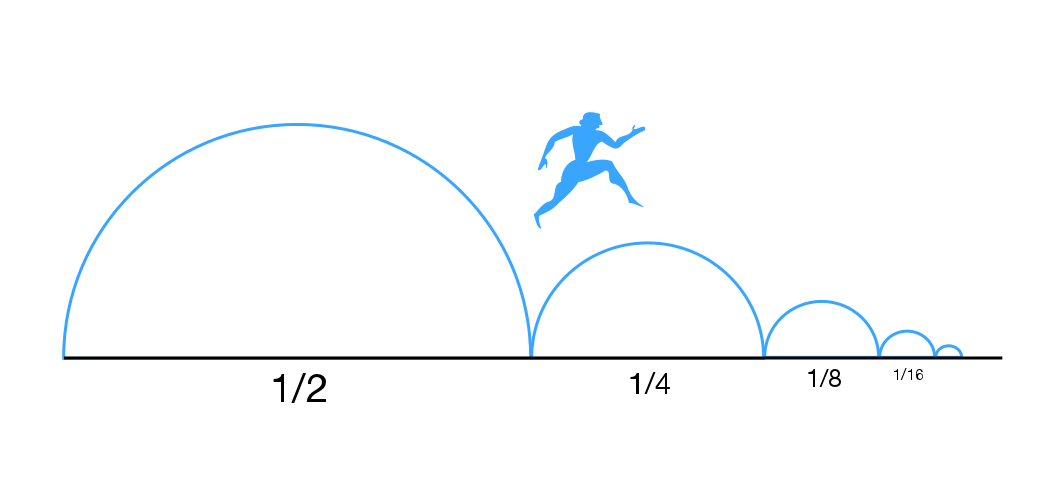
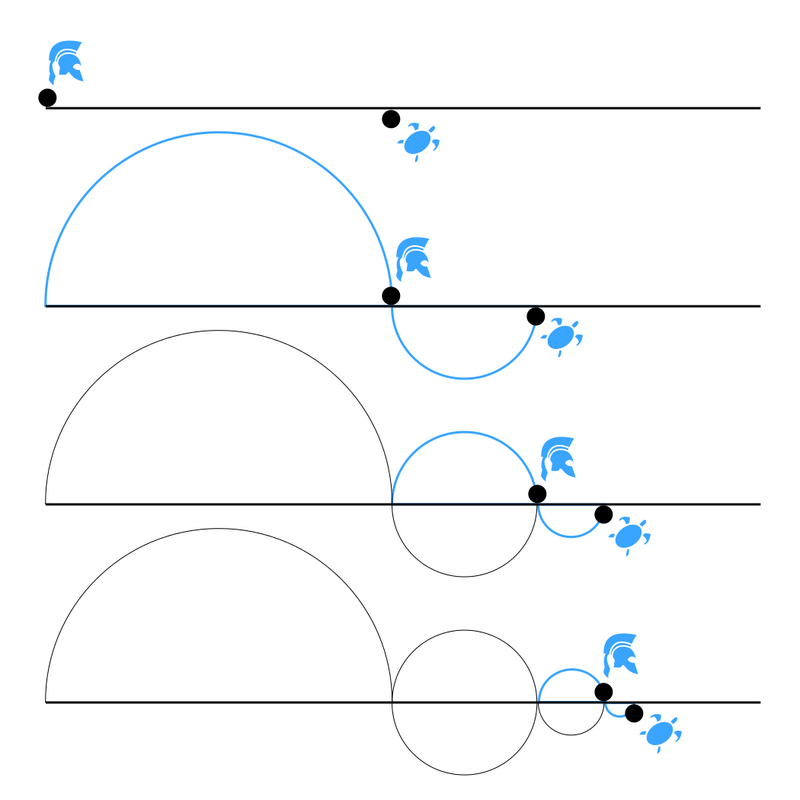
Con ayuda de una calculadora, calcular

$\\frac{1}{2} + \\frac{1}{4} + \\frac{1}{8} + \\frac{1}{16} + \\frac{1}{32} + \\frac{1}{64}$

 

Comparar con $1 - \\frac{1}{64}$

¿Y si no nos detuviéramos nunca?

$\\frac{1}{2} + \\frac{1}{4} + \\frac{1}{8} + \\frac{1}{16} + \\frac{1}{32} + \\frac{1}{64} + \\frac{1}{128} + \\frac{1}{256} + \\frac{1}{512} + \\cdots$

Y si, en vez de partir por la mitad, partiéramos en 10, ¿cuánto vale

$\\frac{1}{10} + \\frac{1}{100} + \\frac{1}{1000} + \\frac{1}{10000} + \\frac{1}{100000} + \\cdots$

Comparar con $\\frac{1}{9}$

Entonces, ¿cuánto vale $\\frac{9}{9} = \\,?$ Y, finalmente, ¿cuánto vale

$\\frac{9}{10} + \\frac{9}{100} + \\frac{9}{1000} + \\frac{9}{10000} + \\frac{9}{100000} + \\cdots = 0,99999\\ldots$

La noción de límite solo se dominó muy recientemente por los matemáticos, a mediados del siglo XIX; por ello, no debe extrañar que existan enfoques muy contrastados: aceptar como evidente y natural que el movimiento es posible —que la flecha alcanzará su blanco— y, al mismo tiempo, rechazar que $0,999\\ldots = 1$.

Sin embargo, desde el punto de vista lógico, es rigurosamente lo mismo. En efecto, aceptamos que

$\\frac{1}{2} + \\frac{1}{4} + \\frac{1}{8} + \\frac{1}{16} + \\frac{1}{32} + \\frac{1}{64} + \\frac{1}{128} + \\frac{1}{256} + \\frac{1}{512} + \\cdots = 1$

lo que se escribe en base dos

$1 = 0,11111\\ldots_b$

y en base diez (la base usual), si

$0,11111\\ldots = \\frac{1}{9}$

no plantea problemas, igual que

$0,33333\\ldots = \\frac{3}{9} = \\frac{1}{3}$

sin embargo, la escritura

$0,99999\\ldots = \\frac{9}{9} = 1$

no es aceptada fácilmente por el alumnado. No obstante, es una igualdad matemática (cuyo tratamiento formal suele exigirse en Bachillerato, después de estudiar progresiones geométricas y sus sumas).