Résumé du conte

Une petite fille offre une oie à la famille royale. Invitée à en faire le partage, elle répartit symboliquement les parties de l’animal, et garde le plus gros morceau pour elle.

Plus tard, elle est appelée à répartir 5 oies entre 7 personnes. Par un raisonnement inventif et rusé, elle réussit à satisfaire tout le monde… et à gagner plusieurs sacs d’or.

À propos du conte

Ce conte a été popularisé sous une forme courte par Léon Tolstoï, notamment dans ses textes éducatifs destinés aux enfants. Il s’inspire d’histoires de sagesse traditionnelles russes ou orientales, illustrant l’intelligence pratique et la ruse face à un tâche difficile.

Le partage des oies illustre :

- une division impossible (5 oies ÷ 7 personnes),

- une ruse narrative,

- et les différentes façons de partager un nombre en parts égales de nombres.

👉 Découvrir le conte

Maths

Divisions, quotients, distribution…
et une jeune fille inventive

👦🏻Âge cible : 9–11 ans (CM1–CM2)
⏰Durée estimée : 1h
📎Matériel : jetons (7 rouges, 5 bleus), papier, figurines.
Prolongement possible : discussions sur le « reste » dans les divisions, jeux de partages, travail sur la décomposition d’un nombre en produit de facteurs.

🎯 Objectifs pédagogiques

• Comprendre la division euclidienne et le rôle du reste.
• Revoir le vocabulaire de la division euclidienne :  dividende, diviseur, quotient et reste.
• Identifier une ruse logique dans une situation bloquée.
• Partager un ensemble d’objets en sous-ensemble de même cardinal.
  

🔢 Notions mathématiques en jeu

• Division euclidienne : $a = b \times q + r$ a = b × q + r (où a est le dividende, b le diviseur, q le quotient, r le reste).

Exemples:

$10 \div 6$ : Le quotient est 1 et le reste 4 ;         on a $10 = 6 \times 1 + 4$

$5 \div 3$ :  Le quotient est 1 et le reste est 2 ;   on a $5 = 3 \times 1 + 2$

$5 \div 2$ :  Le quotient est 2 et le reste est 1 ;   on a $55 = 2 \times 2 + 1$

Ruse : Nous allons voir que la petite fille ajoute le dividende, le diviseur et se compte par la même occasion. La petite fille forme des groupes de 3 ou 4 personnes en intégrant les oies dans le comptage. Elle joue sur l'ambiguïté de la division, parle-t-on du nombre de parts ou de la taille des parts? La division peut être vue comme une partition, un partage d’un tout, on recherche la valeur d’une part, ou bien comme une quotition, un groupement en parts égales dont on recherche le nombre.

🟢 Activité 1. Révision : vocabulaire et pratique de la division euclidienne

1) Rappels de vocabulaire :

- Dividende : nombre que l’on partage
- Diviseur : nombre de parts ou de personnes
- Quotient : nombre d’objets par part
- Reste : ce qui ne peut pas être réparti équitablement

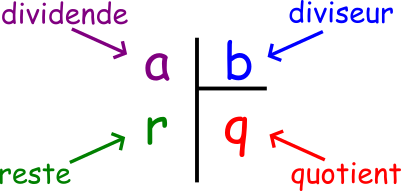
2) Exemples à traiter :

25 ÷ 4 : Le quotient est 6 et le reste est 1 ;

51 ÷ 7 : Le quotient est 7 et le reste est 2 ; 

10 ÷ 6 : Le quotient est 1 et le reste est 4 ;

5 ÷ 2 : Le quotient est 2 et le reste est 1.

Lorsque le reste est zéro, on peut partager l’ensemble de départ en sous-ensembles qui ont tous le même nombre d’éléments. Par exemple, avec 15 fleurs, on peut faire 3 bouquets de 5 fleurs ou 5 bouquets de 3 fleurs.

3) Façons possibles de partager 12 en parts égales : On peut faire manipuler avec des jetons ou du matériel pour bien visualiser les parts. On obtiendra :  

12 = 12 parts de 1

12 = 6 parts de 2

12 = 4 parts de 3

12 = 3 parts de 4

12 = 2 parts de 6

12 = 1 part de 12

🟢 Activité 2. Le premier partage « symbolique ».

Faire rejouer la scène avec une oie et 7 figurines (roi, reine, 2 princes, 2 princesses, la fille pauvre).
Associer symboliquement chaque partie de l’oie à un personnage.

Objectif : comprendre que le partage est narratif, pas mathématique. La fille se place en dehors du calcul, puis s’inclut à la fin.

🟢 Activité 3. Le partage en « 3 » (en réalité : en parts de 3)

La petite fille crée 3 groupes de 2 personnes (roi/reine, 2 princes, 2 princesses), sans se compter.

La division mathématique est : 5 ÷ 3 le quotient est  1 et le reste est 2
→ Une oie est attribuée à chaque groupe de 2 personnes.
→ Les 2 oies restantes reviennent à la fille, selon sa logique : « Les pauvres mangent les restes de la table du roi. »

Mais suivant un autre point de vue, elle compte la famille royale (6 personnes), les oies (5 oies), et elle-même ; ce qui lui fait un total de 12 éléments, avec lesquels elle fait 4  « paquets » de 3.

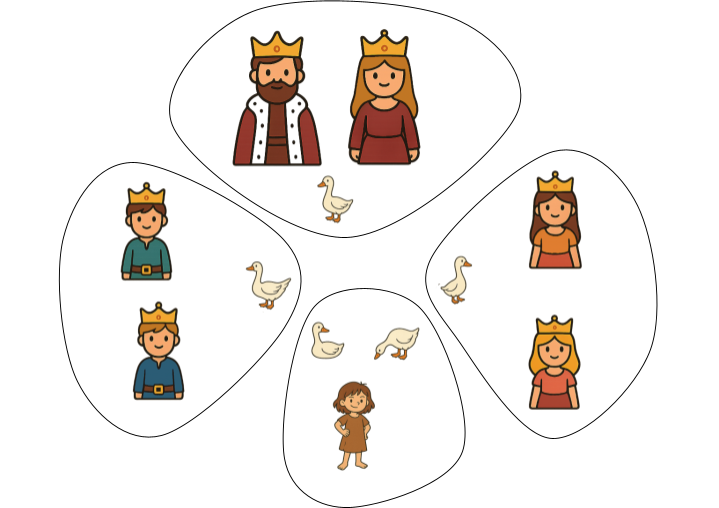
🟢 Activité 3. Le partage en « 4 » (en réalité : en parts de 4)

Elle commence par former deux groupes de 3 personnes parmi la famille royale, tout en se mettant à part. Si elle effectuait la division euclidienne de 5 par 2, étant donné que le quotient est 2 et le reste 1, il lui faudrait, en suivant sa première logique, donner 2 poules à chaque groupe de 3, et prendre une poule pour elle. Mais en procédant ainsi elle ne répondrait pas à la consigne de faire un partage « en 4 », car le nombre 4 n'apparaît nulle part. De plus, le partage n’est pas avantageux pour elle.

Elle utilise donc le partage :  12 = 3 parts de 4

- (reine, 2 princesses, 1 oie)
- (roi, 2 princes, 1 oie)
- (la fille + 3 oies)

Elle fait mine d’oublier son statut de servante qui mange « les restes ».

Activité graphique ou manipulative :
- On peut distribuer des figurines ou des jetons, représentant les membres de la famille royale, les oies et la petite fille, et faire explorer les différentes distributions possibles.

Note : Le premier partage, où elle donne la tête au roi, le cou à la reine, les pattes aux princes et les ailes aux princesses est un motif répandu dans la littérature orale. Suivant les traditions ou les cultures, la part de la mère, notamment, peut varier, ainsi que sa justification : le cou car « elle porte le roi », le cœur ou la poitrine car la mère est  « le cœur du foyer », voire le croupion car « c’est sur elle que tout repose ».