Resumen del cuento

Una niña ofrece una oca a la familia real. Invitada a realizar el reparto, asigna simbólicamente las partes del animal y se guarda para sí el trozo más grande.

Más tarde, la llaman para repartir 5 ocas entre 7 personas. Con un razonamiento ingenioso y astuto, logra satisfacer a todo el mundo… y ganarse varios sacos de oro.

Acerca del cuento

Este cuento fue popularizado en una versión breve por León Tolstói, especialmente en sus textos educativos destinados a la infancia. Se inspira en historias de sabiduría tradicionales rusas u orientales, que ilustran la inteligencia práctica y la astucia frente a una tarea difícil.

El reparto de las ocas ilustra:

– una división imposible (5 ocas ÷ 7 personas),

– una astucia narrativa,

– y las distintas maneras de repartir un número en partes iguales de cantidades.

👉 Descubrir el cuento

Maths

Divisiones, cocientes, distribución…
y una joven ingeniosa

👦🏻 Edad objetivo: 9–11 años (CM1–CM2)
⏰ Duración estimada: 1 h
📎 Material: fichas (7 rojas, 5 azules), papel, figuritas.
Posible prolongación: debates sobre el «resto» en las divisiones, juegos de reparto, trabajo sobre la descomposición de un número en producto de factores.

🎯 Objetivos pedagógicos

• Comprender la división euclidiana y el papel del resto.
• Revisar el vocabulario de la división euclidiana: dividendo, divisor, cociente y resto.
• Identificar una astucia lógica en una situación bloqueada.
• Repartir un conjunto de objetos en subconjuntos con el mismo cardinal.

🔢 Nociones matemáticas en juego

• División euclidiana: $a = b \times q + r$ (donde $a$ es el dividendo, $b$ el divisor, $q$ el cociente y $r$ el resto).

Ejemplos:

$10 \div 6$: el cociente es 1 y el resto 4;   tenemos $10 = 6 \times 1 + 4$

$5 \div 3$: el cociente es 1 y el resto es 2;  tenemos $5 = 3 \times 1 + 2$

$5 \div 2$: el cociente es 2 y el resto es 1;  tenemos $5 = 2 \times 2 + 1$

Astucia: veremos que la niña añade el dividendo, el divisor… ¡y se cuenta a sí misma de paso! La niña forma grupos de 3 o de 4 personas integrando las ocas en el conteo. Juega con la ambigüedad de la división: ¿hablamos del número de partes o del tamaño de las partes? La división puede verse como una partición, el reparto de un todo (buscamos el valor de una parte), o como una cocienteación (quotition), un agrupamiento en partes iguales del que buscamos el número.

🟢 Actividad 1. Repaso: vocabulario y práctica de la división euclidiana

1) Recordatorio de vocabulario:

– Dividendo: número que se reparte
– Divisor: número de partes o de personas
– Cociente: número de objetos por parte
– Resto: lo que no puede repartirse equitativamente

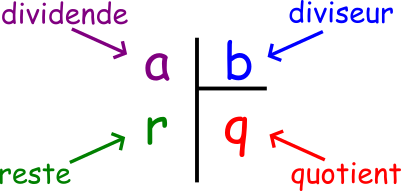
2) Ejemplos a resolver:

25 ÷ 4: el cociente es 6 y el resto es 1;

51 ÷ 7: el cociente es 7 y el resto es 2;

10 ÷ 6: el cociente es 1 y el resto es 4;

5 ÷ 2: el cociente es 2 y el resto es 1.

Cuando el resto es cero, el conjunto inicial puede repartirse en subconjuntos que tienen todos el mismo número de elementos. Por ejemplo, con 15 flores podemos hacer 3 ramos de 5 flores o 5 ramos de 3 flores.

3) Maneras posibles de repartir 12 en partes iguales: se puede manipular con fichas u otro material para visualizar bien las partes. Obtendremos:

12 = 12 partes de 1

12 = 6 partes de 2

12 = 4 partes de 3

12 = 3 partes de 4

12 = 2 partes de 6

12 = 1 parte de 12

🟢 Actividad 2. El primer reparto «simbólico»

Representar la escena con una oca y 7 figuritas (rey, reina, 2 príncipes, 2 princesas, la niña pobre).
Asociar simbólicamente cada parte de la oca con un personaje.

Objetivo: comprender que el reparto es narrativo, no matemático. La niña se coloca fuera del cálculo y después se incluye al final.

🟢 Actividad 3. El reparto en «3» (en realidad: en partes de 3)

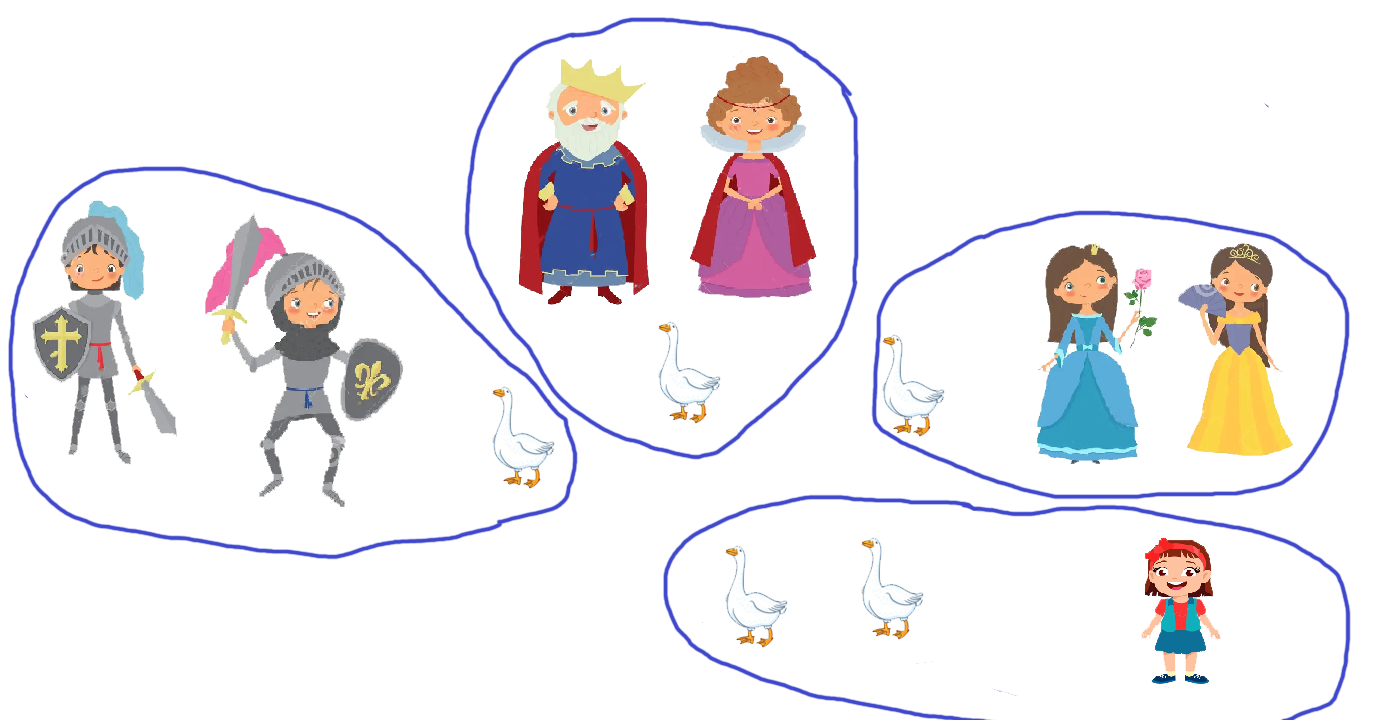
La niña crea 3 grupos de 2 personas (rey/reina, 2 príncipes, 2 princesas), sin contarse a sí misma.

La división matemática es: 5 ÷ 3, el cociente es 1 y el resto es 2.
→ Una oca se atribuye a cada grupo de 2 personas.
→ Las 2 ocas restantes van para la niña, según su lógica: «Los pobres comen los restos de la mesa del rey».

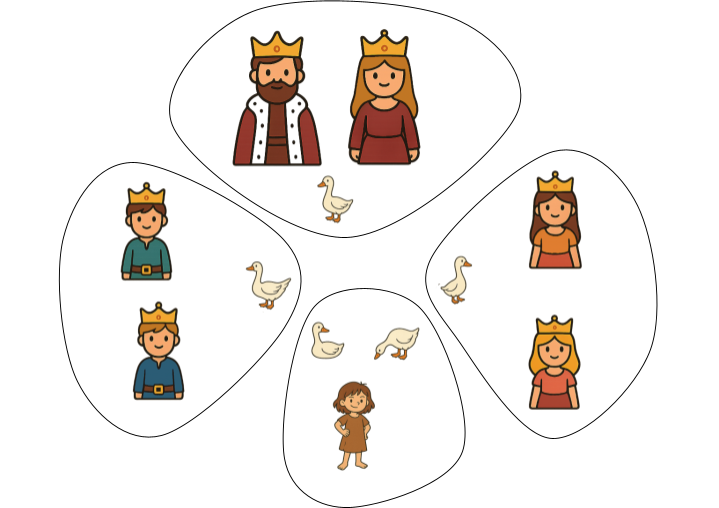
Pero desde otro punto de vista, cuenta a la familia real (6 personas), las ocas (5 ocas) y a sí misma; lo que hace un total de 12 elementos, con los que forma 4 «paquetes» de 3.

🟢 Actividad 3. El reparto en «4» (en realidad: en partes de 4)

Empieza formando dos grupos de 3 personas dentro de la familia real, quedándose aparte. Si efectuara la división euclidiana de 5 entre 2, dado que el cociente es 2 y el resto 1, siguiendo su primera lógica debería dar 2 gallinas a cada grupo de 3 y quedarse una para ella. Pero así no respondería a la consigna de hacer un reparto «en 4», porque el número 4 no aparece por ninguna parte. Además, el reparto no le sería ventajoso.

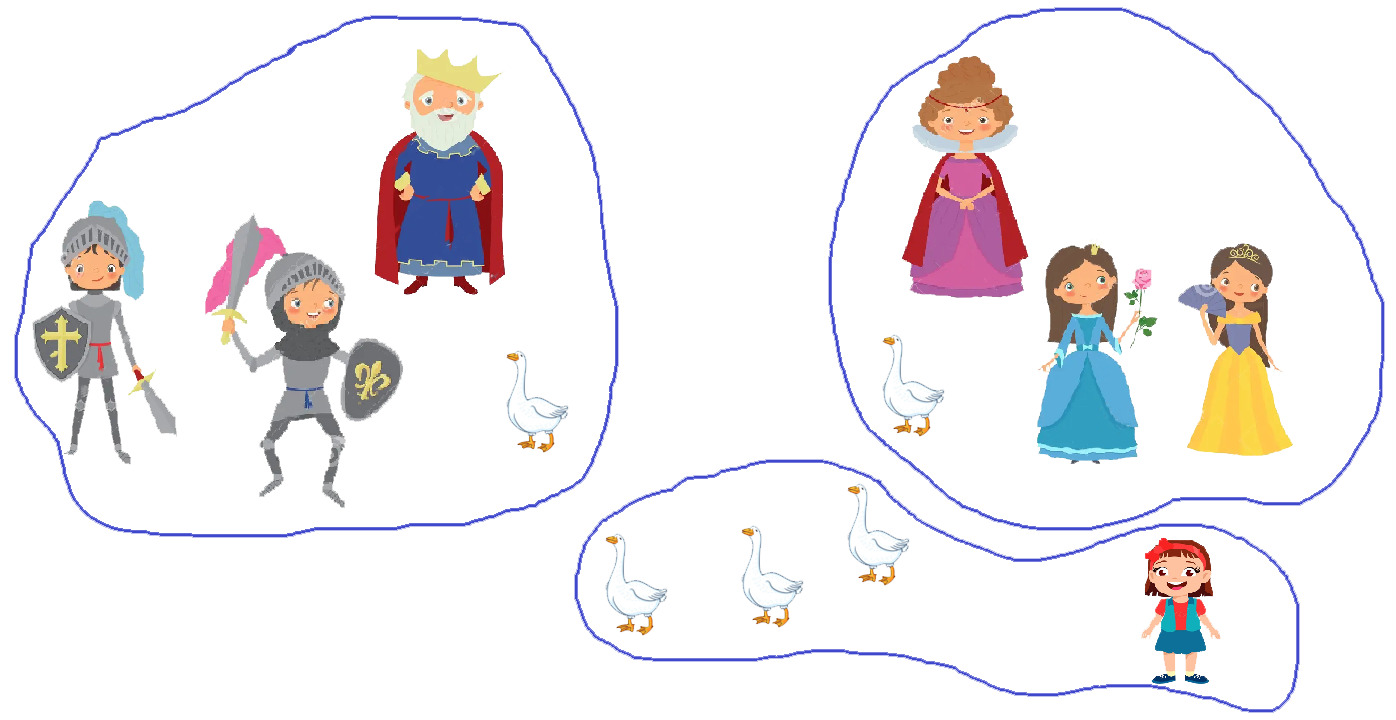
Utiliza, pues, el reparto: 12 = 3 partes de 4

– (reina, 2 princesas, 1 oca)
– (rey, 2 príncipes, 1 oca)
– (la niña + 3 ocas)

Finge olvidar su condición de sirvienta que come «los restos».

Actividad gráfica o manipulativa:
– Se pueden distribuir figuritas o fichas que representen a los miembros de la familia real, las ocas y la niña, y explorar las distintas distribuciones posibles.

Nota: el primer reparto —cabeza para el rey, cuello para la reina, patas para los príncipes y alas para las princesas— es un motivo extendido en la literatura oral. Según tradiciones o culturas, la parte de la madre, en particular, puede variar, así como su justificación: el cuello porque «sostiene al rey», el corazón o el pecho porque la madre es «el corazón del hogar», o incluso el rabadillo porque «sobre ella descansa todo».