A box has a shape and a capacity. The myth begins with Horus being placed in a sarcophagus. Some candidates are too tall, others too wide, others too small. Only Horus fits perfectly into this specially built box. Here are some boxes. How can they be classified? In terms of volume?

First, there will be simple cases: one box fits entirely inside another. Then more complex cases: a thin box fits inside a wider one but exceeds in height. Students often focus on a single dimension and consider the longest box as the largest. The ambiguity is resolved by filling one with semolina and pouring it into the other. If it all fits, the second is bigger; if it overflows, the first is bigger.

Using a calculator, compute $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64}$

Compare with $1 - \frac{1}{64}$

On a paper strip (used as one unit), fold to mark half, then a quarter, an eighth, a sixteenth… Understand visually how each step decomposes the unit:

$1 = \frac{1}{2} + \frac{1}{2} = \frac{1}{2} + \frac{1}{4} + \frac{1}{4} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{8} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{16} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{32} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{64}$

Cut the unit strip:

Then measure each proposed strip using only these small strips and write down your results.

Prepare vertical A4 strips and simple fractions. Have students observe that:

$\frac{3}{4} = \frac{1}{2} + \frac{1}{4}, \quad \frac{5}{8} = \frac{1}{2} + \frac{1}{8}, \quad \frac{3}{8} = \frac{1}{4} + \frac{1}{8}, \quad \frac{1}{3} = \frac{1}{4} + \frac{1}{16} + \frac{1}{64} + \cdots, \quad \frac{2}{3} = \frac{1}{2} + \frac{1}{8} + \frac{1}{32} + \cdots$

For the last ones, construct using a square or equilateral triangle divided into four similar shapes and repeat inside. The total area is split into thirds—red, blue, green—which are themselves composed of quarters, sixteenths, sixty-fourths, etc. Great constructions and a taste of infinity.

Another version of the paradox is Zeno of Elea's, showing that nothing changes in the world: Achilles, the fastest Greek hero, will never catch the tortoise. First, he must reach the tortoise's starting point, but meanwhile, the tortoise moves a little. The same reasoning applies. Similarly, the arrow (or runner) will never reach its target, because to reach it, it must first travel half the distance, then half of the remaining half, then a quarter, an eighth, a sixteenth, etc.

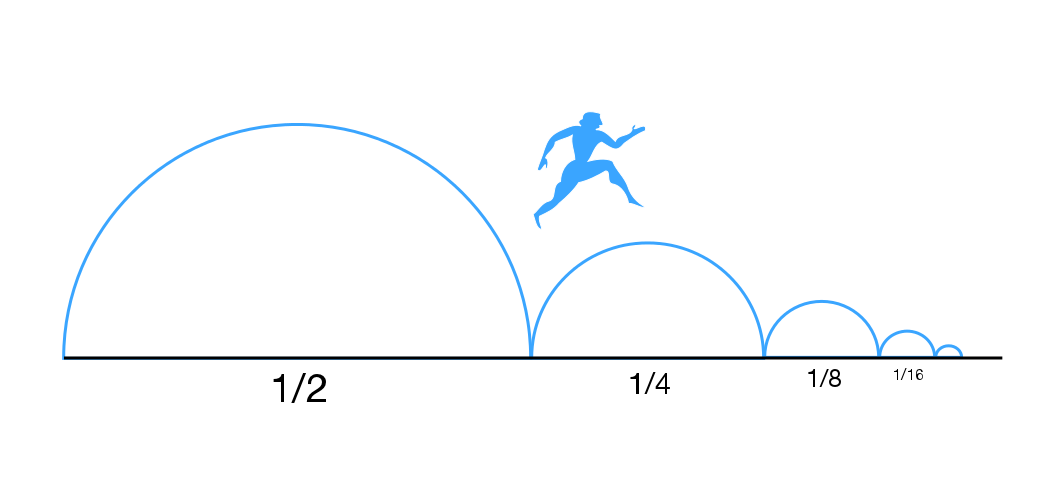
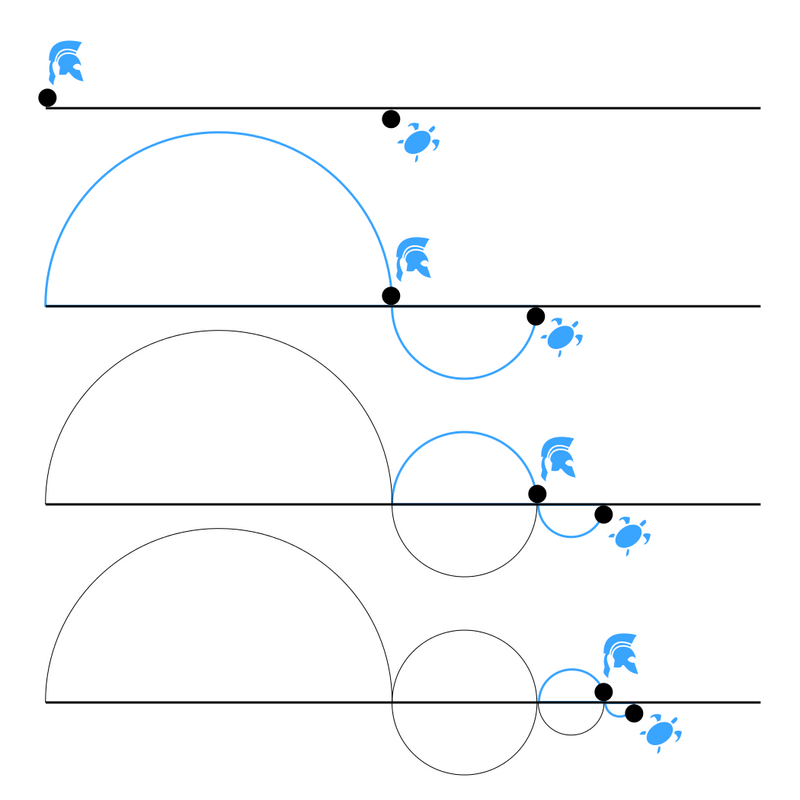
Using a calculator, compute:

$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64}$

Compare with $1 - \frac{1}{64}$

If we continue:

$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{128} + \frac{1}{256} + \frac{1}{512} + \cdots$

And if we divided by 10 instead of 2, what is:

$\frac{1}{10} + \frac{1}{100} + \frac{1}{1000} + \frac{1}{10000} + \frac{1}{100000} + \cdots$

Compare with $\frac{1}{9}$

Then, what is $\frac{9}{9} = ?$ And finally, what is:

$\frac{9}{10} + \frac{9}{100} + \frac{9}{1000} + \frac{9}{10000} + \frac{9}{100000} + \cdots = 0.99999\ldots$

The notion of a limit was only rigorously developed by mathematicians in the mid-19th century. Students may have contrasting approaches: some accept that motion is possible and the arrow reaches its target; others reject that $0.999\ldots = 1$, even though logically it is the same. Indeed,

$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \cdots = 1$

which in base 2 is:

$1 = 0.11111\ldots_2$

In base 10:

$0.11111\ldots = \frac{1}{9}$

just as

$0.33333\ldots = \frac{3}{9} = \frac{1}{3}$

and

$0.99999\ldots = \frac{9}{9} = 1$

is mathematically correct, though students often do not accept it. This equality is formally introduced after studying geometric series and their sums.