Myths
Dido's Ruse
Story Summary
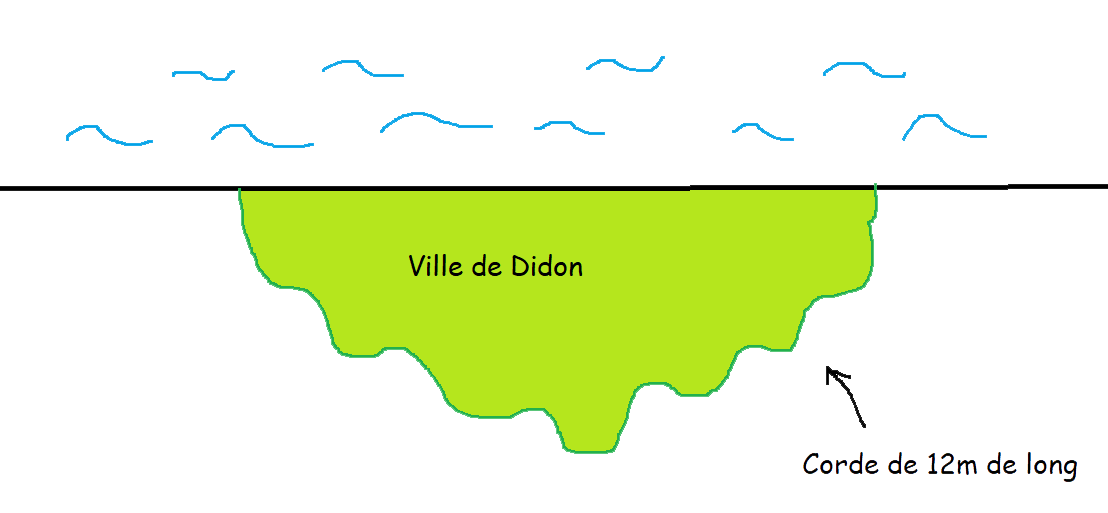
Dido, a princess of Phoenicia, flees her kingdom after the assassination of her husband. Arriving in North Africa (in Numidia, present-day Tunisia), she negotiates a strange condition with the local king: to receive as much land as can be covered by an ox hide.
Through clever cutting, she turns this constraint into an advantage: she traces a vast semicircle along the seashore, founds the city of Carthage... and gives history a lesson in geometry!
About the Story
This legendary tale tells of the founding of a city—but also of a ruse, a negotiation, and an astonishing geometric intuition!
The story is easy to tell: it follows a clear sequence of actions, with a clever female character, a challenge posed, and a surprising solution.
It's a great starting point for discussing geometry, as well as logic and strategy.
Students love the twist: the king thinks he has won... but Dido had planned everything!
👉 Discover the Story
Maths
Perimeters, Areas...
and a Very Clever Queen
🔢 Mathematical Concepts Involved
- Calculating magnitudes: perimeter, area of common shapes (rectangle, square, circle)
- Relationship between perimeter and area
- Properties of circles and disks
- Modeling
- Using formulas
- Problem-solving.
📋 Prerequisites
- Know the units of length and area (and their subdivisions)
- Know how to calculate the area and perimeter of a rectangle, square, and circle (see appendix).
🟢 Activity 1. Cut Like Dido!
👦🏻 Target Age: 8-10 years (Grades 3-5)
⏰ Duration: 20 min
📎 Materials: one A4 sheet per student or pair
🎯 Objective
Replicate Dido's action by cutting an A4 sheet into a continuous strip to form a circular area.
🗣️ Instructions for Students
Dido managed to obtain a large piece of land from an ox hide. But how? By cutting it into a long strip to trace a circle. Let's try to do the same!
Fold your sheet cleverly so you can cut it into one long strip. The thinner the strip, the longer it is!

💬 Pedagogical Comments
You can vary several parameters:
• The size of the sheet (representing the ox hide)
• The width of the strip.
Observe what changes:
• What happens if you reduce the width of the strip?
• What happens if you change the size of the sheet?
• What varies, what remains constant?
This activity naturally introduces the concept of parameters.
Students discover that the length of the strip depends on its width and the initial surface—and that a given perimeter can enclose a variable area.
🟢 Activity 2. What Shape for Carthage? (with Rectangles)
👦🏻 Target Age: 9-10 years (Grades 4-5)
⏰ Duration: 30 min
🎯 Objective
Among several rectangles, find the shape that allows building the largest area using a 12 m rope. One side is bordered by the sea!
🗣️ Instructions for Students
Dido wanted to found a city using an ox hide cut into a strip. Now it's your turn to imagine the ideal shape to build Carthage with a 12 m rope. The sea forms one side of the land. Your turn!
Test 1: rectangle with 1 meter width
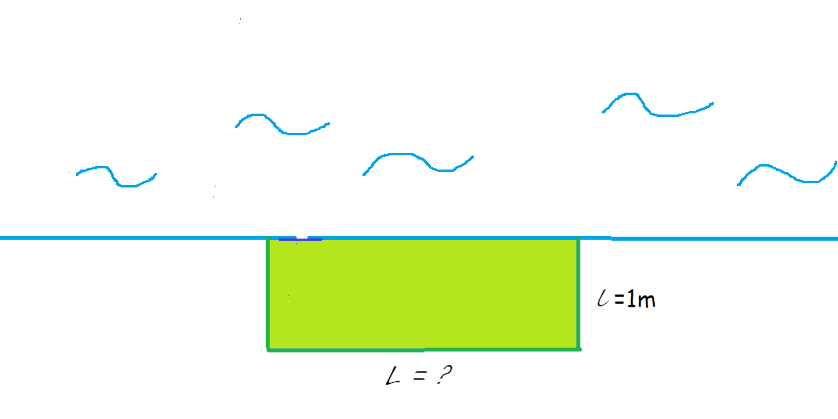
What is the length L of this rectangle?
What is the area of this rectangle?
Test 2: rectangle with 2 m width
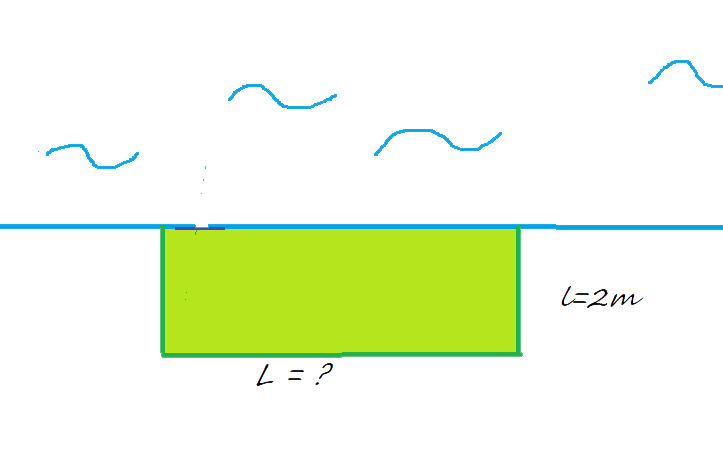
Length L = ?
Area = ?
Test 3: rectangle with 3 m width
Length L = ?
Area = ?
Test 4: rectangle with 4 m width.
Length L = ?
Area = ?
Test 5: rectangle with 5 m width.
Length L = ?
Area = ?
Test 6: with a rectangle of 6 m width, will the area be larger or smaller than the previous rectangles?
✅ Conclusion:
Which shape gives the largest area?
If you were Dido, what shape would you have chosen to found your city?
🟢 Activity 3. Dido's Semicircle
👦🏻 Target Age: 10-11 years (Grade 5 - 6)
⏰ Duration: 30 min
🎯 Objective
With a 12m rope, create a shape with the largest possible area, knowing that one side will be along the sea. Calculate the area if you build, like Dido, a semicircle along the sea.

🗣️ Instructions for Students
• With the help of the "Appendix" sheet, find the radius of this semicircle.
• Calculate the area of the semicircle.
Conclusion: With a rope of given length, what is the best design for Dido's city?
🔢 Appendix – Useful Formulas
Rectangle
-
Perimeter of a rectangle:
$P = 2 × (L+w)$
where L is the length and w is the width -
Area of a rectangle:
$A = L × w$
Circle
-
Perimeter of a circle:
$P = 2 × π × r$ -
Area of a circle:
$A = π × r^2$
Perimeters, Areas, and Geometric Ruse
(Teacher's Sheet)
With a 12 m rope, we want to create a shape with the largest possible area, knowing that one side will be along the sea:

We will try with rectangles and squares (Activity 2), then with a semicircle (Activity 3).
🟣 Activity 2. Rectangles and Squares

Test 1: width = 1 m
Calculate the length L of this rectangle. $L = 10 m$
Calculate the area of this rectangle $A = 10 m^2$
Test 2: width = 2 m
Calculate the length L of this rectangle. $L = 8 m$
Calculate the area of this rectangle. $A = 16 m^2$
Test 3: width = 3 m
Calculate the length L of this rectangle. $L = 6 m$
Calculate the area of this rectangle. $A = 18 m^2$
Test 4: width = 4 m
Calculate the length L of this rectangle. $L = 4 m$. What is its special shape? $Square$
Calculate the area of this rectangle. $A = 16 m^2$
Test 5: width = 5 m
Calculate the length L of this rectangle. $L = 2 m$
Calculate the area of this rectangle. $A = 10 m^2$
Test 6: width = 6 m
Both widths use up all the rope, nothing is left for the length. $A = 0 m^2$
Test |
Width (m) |
Length (m) |
Area (m²) |
Remark |
1 |
1 |
10 |
10 |
|
2 |
2 |
8 |
16 |
Area increases |
3 |
3 |
6 |
18 |
🔺 Maximum |
4 |
4 |
4 |
16 |
Square |
5 |
5 |
2 |
10 |
Area decreases |
6 |
6 |
❌ Impossible (no rope left) |
🟣 Activity 3. Semicircle
We want to find the area achieved if we build, like Dido, a semicircle along the sea.

- Using the "Appendix" section, find the radius of this semicircle.
$r = \frac{12}{\pi} \approx 3.81 m$
- Calculate the area of the semicircle.
$A = \frac{1}{2} \pi r^2 = \frac{\pi \times 3.81^2}{2} = 22.91 m^2$
✅ Conclusion
With a rope of given length, what seems to be the best design for Dido's city?
The best design for Dido's city seems to be the circle.

