Митовe
Хитростта на Дидона
Резюме на разказа
Дидона, принцеса на Финикия, бяга от царството си след убийството на съпруга си. Пристига в Северна Африка (в Нумидия, днешна Тунис), където преговаря с местния цар за странно условие: да получи толкова земя, колкото може да покрие една биволска кожа.
Благодарение на хитро изрезване, тя превръща това ограничение в предимство: очертава обширна полукръгла територия на брега на морето, основава града Картаген ... и дава на историята урок по геометрия!
За разказа
Този легендарен разказ разказва за основаването на град - но също и за хитрост, преговори и изненадваща геометрична интуиция!
Историята е лесна за разказване: тя следва серия от ясни действия, с умна женска фигура, поставено предизвикателство и изненадващо решение.
Това е добра отправна точка за разговор за геометрия, но също и за логика и стратегия.
Учениците харесват обръта: царят мисли, че е спечелил ... но Дидонаше го предвидила всичко!
👉 Откриване на разказа
Математика
Периметри, площи...
и една много хитроумна царица
🔢 Математически понятия в игра
- Изчисляване на величини: периметър, лице на обикновени повърхности (правоъгълник, квадрат, кръг)
- Връзка между периметър и площ
- Свойства на кръга и диска
- Моделиране
- Използване на формули
- Решаване на проблеми.
📋 Предварителни изисквания
- Познаване на единиците за дължина и площ (и техните подразделения)
- Знаене как да се изчисли площта и периметъра на правоъгълник, квадрат, кръг (вижте приложението).
🟢 Дейност 1. Изрежи като Дидона!
👦🏻 Възрастова група: 8-10 години (II - IV клас)
⏰ Продължителност: 20 мин
📎 Материали: един лист A4 за ученик или двойка
🎯 Цел
Повторете жеста на Дидона, като изрежете лист A4 на непрекъсната лента, за да оформите кръгла площ.
🗣️ Инструкции за учениците
Дидона успя да получи голям терен от една биволска кожа. Но как? Тя я наряза на дълъг ивица, за да очертае кръг. Ако опитваме да направим същото?
Сгънете хитро листа си, за да можете да го изрежете на една дълга лента. Колкото по-тънка е лентата, толкова по-дълга е!

💬 Педагогически бележки
Можете да варитерате няколко параметъра:
• Размера на листа (представляващ биволската кожа)
• Ширината на лентата.
Наблюдавайте какво се променя:
• Какво се случва, ако намалим ширината на лентата?
• Какво се случва, ако променим размера на листа?
• Какво се променя, какво остава постоянно?
Това манипулиране въвежда естествено понятието параметри.
🟢 Дейност 2. Каква форма за Картаген? (с правоъгълници)
👦🏻 Възрастова група: 9-10 години (III/IV клас)
⏰ Продължителност: 30 мин
🎯 Цел
Намерете, сред няколко правоъгълника, формата, която позволява да построите най-голямата площ, използвайки 12 м въже. Една от страните е оградена от морето!
🗣️ Инструкции за учениците
Дидона искаше да основа град, използвайки биволска кожа, нарязана на лента. Сега е твой ред да си представиш идеалната форма за построяване на Картаген с 12 м въже. Морето образува една от страните на парцела. На теб ти е вряме!
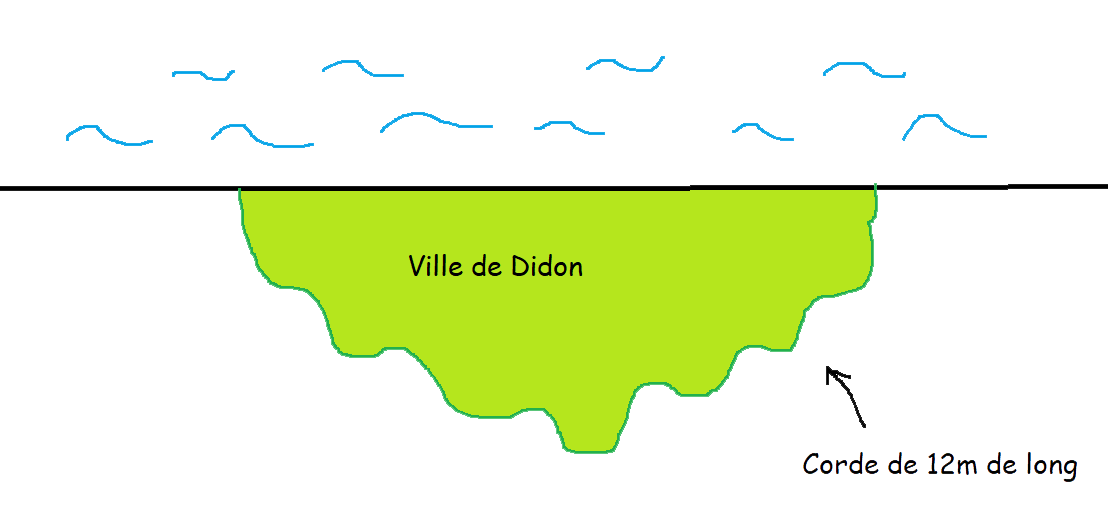
Опит 1: правоъгълник с широчина 1 метър
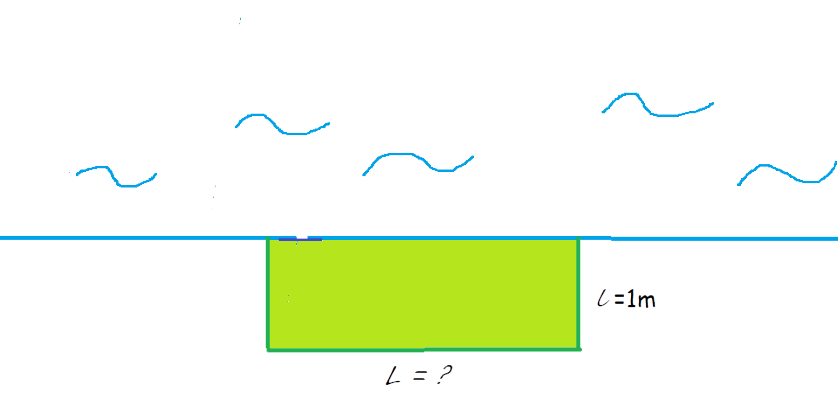
Каква е дължината L на този правоъгълник?
Каква е площта на този правоъгълник?
Опит 2: правоъгълник с ширина 2 м
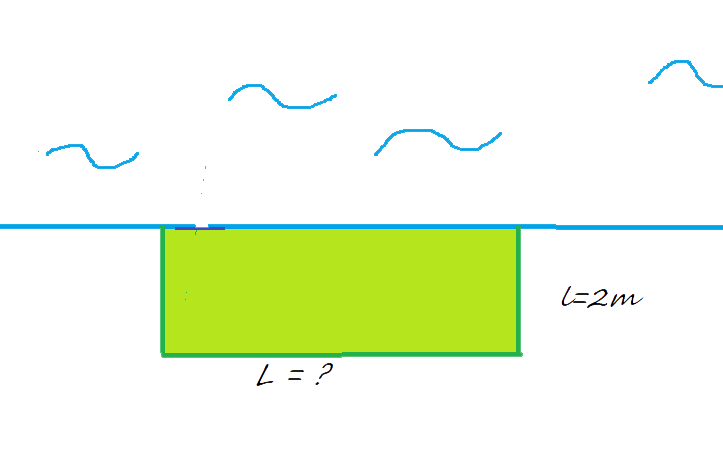
Дължина L = ?
Площ = ?
Опит 3: правоъгълник с ширина 3 м
Дължина L = ?
Площ = ?
Опит 4: правоъгълник с ширина 4 м.
Дължина L = ?
Площ = ?
Опит 5: правоъгълник с ширина 5 м.
Дължина L = ?
Площ = ?
Опит 6: с правоъгълник с ширина 6 м, площта ще бъде по-голяма или по-малка от тези на предходните правоъгълници?
✅ Заключение:
Коя фигура дава най-голямата площ?
Ако беше Дидона, каква форма би избрал за основаването на града си?
🟢 Дейност 3. Полукръгът на Дидона
👦🏻 Възрастова група: 10-11 години (IV клас - VI клас)
⏰ Продължителност: 30 мин
🎯 Цел
С 12 м въже, създайте форма с възможно най-голяма площ, като знаете, че една от страните ще бъде прилежаща към морето. Изчислете площта, ако построите, както Дидона, полукръг, прилегал към морето.

🗣️ Инструкции за учениците
• С помощта на листа "Приложение", намери радиуса на този полукръг.
• Изчисли площта на полукръга.
Заключение: С дадена дължина на въжето, какъв е най-добрият дизайн за града на Дидона?
🔢 Приложение - полезни формули
Правоъгълник
- Периметър на правоъгълник:
$P = 2 × (L+l)$
където L е дължината и l е ширината - Площ на правоъгълник:
$A = L × l$
Кръг
- Периметър на кръг:
$P = 2 × π × r$ - Площ на кръг:
$A = π × r2$
Периметри, площи и геометрическа хитрост
(информация за учителя)
С 12 м въже искаме да създадем форма с възможно най-голяма площ, като знаем, че една от страните ще бъде прилежаща към морето:

Ще направим опити с правоъгълници и квадрати (дейност 2), след това с полукръг (дейност 3).
🟣 Дейност 2. Правоъгълници и квадрати

Опит 1: ширина = 1 м
Изчисли дължината L на този правоъгълник. $L = 10\,m$
Изчисли площта на този правоъгълник $A = 10\,m^2$
Опит 2: ширина = 2 м
Изчисли дължината L на този правоъгълник. $L = 8\,m$
Изчисли площта на този правоъгълник. $A = 16\,m^2$
Опит 3: ширина = 3 м
Изчисли дължината L на този правоъгълник. $L= 6\,m$
Изчисли площта на този правоъгълник. $A = 18\,m^2$
Опит 4: ширина = 4 м
Изчисли дължината L на този правоъгълник. $L = 4\,m$. Каква е неговата специална форма? $Квадрат$
Изчисли площта на този правоъгълник. $A = 16\,m^2$
Опит 5: ширина = 5 м
Изчисли дължината L на този правоъгълник. $L = 2\,m$
Изчисли площта на този правоъгълник. $A = 10\,m^2$
Опит 6: ширина = 6 м
Двете ширини изразходват цялото въже, няма нищо остава за дължината. $A = 0\,m^2$
Опит | Ширина (m) | Дължина (m) | Площ (m²) | Бележка |
1 | 1 | 10 | 10 | |
2 | 2 | 8 | 16 | Площта се увеличава |
3 | 3 | 6 | 18 | 🔺 Максимум |
4 | 4 | 4 | 16 | Квадрат |
5 | 5 | 2 | 10 | Площта намалява |
6 | 6 | ❌ Невъзможно (няма повече въже) |
🟣 Дейност 3. Полукръг
Искаме да намерим площта, ако построим, както Дидона, полукръг, прилегал към морето.

- С помощта на частта "Приложение", намери радиуса на този полукръг.
$r = \frac{12}{\pi} \approx 3{,}81\,m$
- Изчисли площта на полудиска.
$A = \frac{1}{2} \pi r^2 = \frac{\pi \times 3{,}81^2}{2} = 22{,}91\,m^2$
✅ Заключение
С дадено въже с дадена дължина, каква изглежда най-добрата форма за града на Дидона?
Най-добрата форма за града на Дидона изглежда е кръгът.

