Резюме на приказката

Едно малко момиче подарява гъска на кралското семейство. Поканена да я раздели, тя символично разпределя частите от животното и запазва най-голямата част за себе си.

По-късно е помолена да раздели 5 гъски между 7 души. Чрез изобретателно и хитроумно разсъждение, тя успява да задоволи всички... и да спечели няколко чанти злато.

За приказката

Тази приказка е популяризирана в кратък вариант от Лев Толстой, особено в неговите образователни текстове, предназначени за деца. Тя се вдъхновява от традиционни руски или източни истории за мъдрост, илюстриращи практическия ум и хитростта, когато трябва да се реши трудна задача.

Разделянето на гъските илюстрира:

- невъзможно деление (5 гъски ÷ 7 души),

- разказна хитрост,

- и различни начини за разделяне на число на равни части от числа.

👉 Прочетете приказката

Математика

Делене, частно, разпределение...
и едно изобретателно момиче

👦🏻Целева възраст: 9–11 години (4.–5. клас)
⏰Предвидено време: 1 час
📎Материали: жетони (7 червени, 5 сини), хартия, фигури.
Възможно продължение: дискусии за „остатъка“ при деления, игри на разпределение, работа върху разлагането на число на произведение от множители.

🎯 Образователни цели

• Разбиране на евклидовото деление и ролята на остатъка.
• Повторение на терминологията на евклидовото деление: делимо, делител, частно и остатък.
• Разпознаване на логическа уловка в затруднена ситуация
• Разделяне на множество от обекти на подмножества с еднакъв брой елементи.
  

🔢 Математически понятия

• Евклидово деление: $a=b\times q+r$ (където a е делимото, b е делителят, q е частното, r е остатъка).

Примери:

$10÷6$ : Частното е 1 и остатъкът е 4 ;         имаме $10=6\times 1+4$

$5÷3$ :  Частното е 1 и остатъкът е 2 ;   имаме $5=3\times 1+2$

$5÷2$ :  Частното е 2 и остатъкът е 1 ;   имаме $5=2\times 2+1$

Хитрост: Ще видим, че малкото момиче добавя делимото, делителя и се брои заедно с тях. Момичето образува групи от 3 или 4 души, включвайки гъските в броенето. Тя играе с двусмислеността на делението – говорим ли за броя на частите или за размера на частите? Делението може да се разглежда като разделяне на цяло, търсейки стойността на една част, или като групиране на равни части, търсейки броя им.

🟢 Дейност 1. Повторение: терминология и практика на евклидовото деление

1) Повторение на терминологията:

- Делимо: числото, което се дели
- Делител: броят на частите или хората
- Частно: броят на обектите на част
- Остатък: това, което не може да се разпредели равномерно

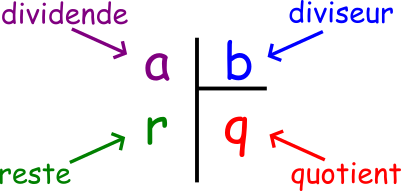
2) Примери за обработка:

25 ÷ 4 : Частното е 6 и остатъкът е 1 ;

51 ÷ 7 : Частното е 7 и остатъкът е 2 ; 

10 ÷ 6 : Частното е 1 и остатъкът е 4 ;

5 ÷ 2 : Частното е 2 и остатъкът е 1.

Когато остатъкът е нула, можем да разделим началното множество на подмножества, които имат еднакъв брой елементи. Например, с 15 цветя, можем да направим 3 букета от по 5 цветя или 5 букета от по 3 цветя.

3) Възможни начини за разделяне на 12 на равни части: Може да се използва материал за визуализация на частите. Ще получим:  

12 = 12 части от по 1

12 = 6 части от по 2

12 = 4 части от по 3

12 = 3 части от по 4

12 = 2 части от по 6

12 = 1 част от 12

🟢 Дейност 2. Първото „символично“ разделяне.

Да се преиграе сцената с една гъска и 7 фигури (крал, кралица, 2 принца, 2 принцеси, бедното момиче).
Да се асоциира символично всяка част от гъската с един персонаж.

Цел: да се разбере, че разделянето е разказно, а не математическо. Момичето се поставя извън изчислението, а после се включва в края.

🟢 Дейност 3. Разделянето на „3“ (всъщност: на части от по 3)

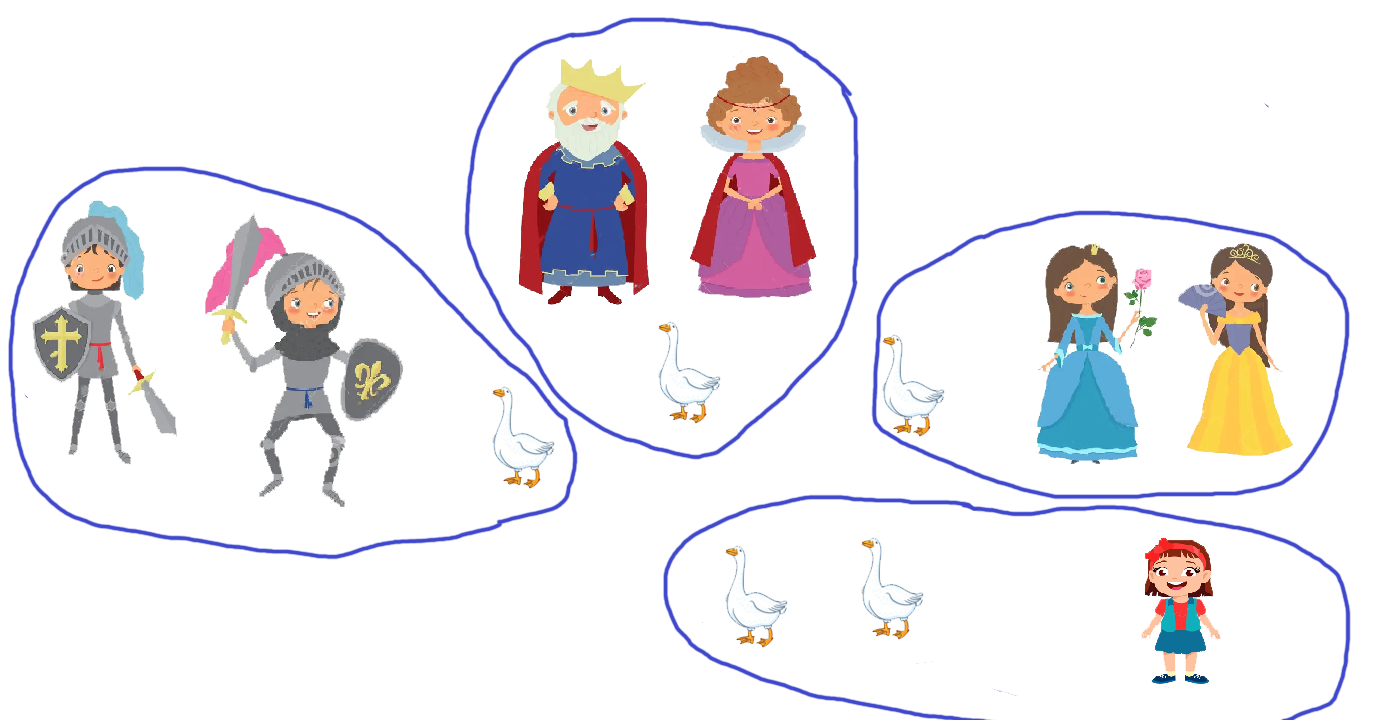
Малкото момиче създава 3 групи от по 2 души (крал/кралица, 2 принца, 2 принцеси), без да се брои.
Математическото деление е: 5 ÷ 3, частното е 1 и остатъка е 2
→ По една гъска се дава на всяка група от 2 души.
→ Двете останали гъски отиват при момичето, според нейната логика: „Бедните ядат остатъците от кралската маса.“

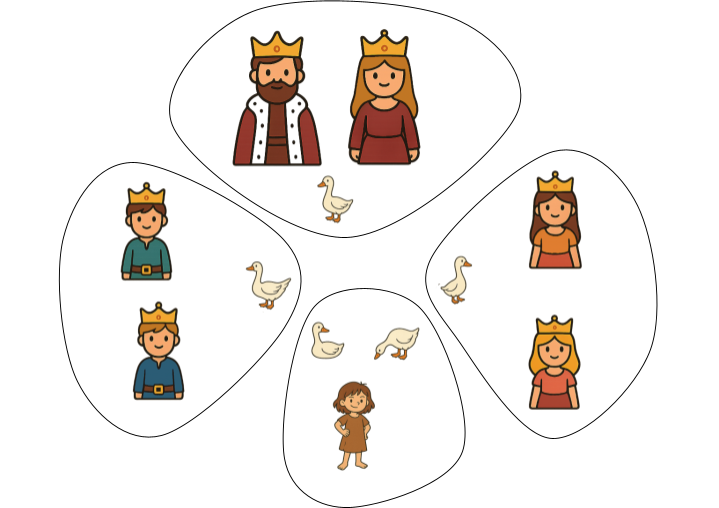
Но от друга гледна точка, тя брои кралското семейство (6 души), гъските (5 гъски) и себе си; което ѝ прави общо 12 елемента, с които прави 4 „пакета“ от по 3.

🟢 Дейност 4. Разделянето на „4“ (всъщност: на части от по 4)

Тя започва с образуването на две групи от по 3 души от кралското семейство, като се държи настрана. Ако беше извършила евклидово деление на 5 на 2, като частното е 2 и остатъка е 1, според първата ѝ логика, трябваше да даде по 2 гъски на всяка група от 3 и да вземе една гъска за себе си. Но така не би отговорила на задачата да раздели „на 4“, защото числото 4 не се появява никъде. Освен това, разделянето не е изгодно за нея.

Тя използва разделянето:  12 = 3 части от по 4

- (кралица, 2 принцеси, 1 гъска)
- (крал, 2 принца, 1 гъска)
- (момичето + 3 гъски)

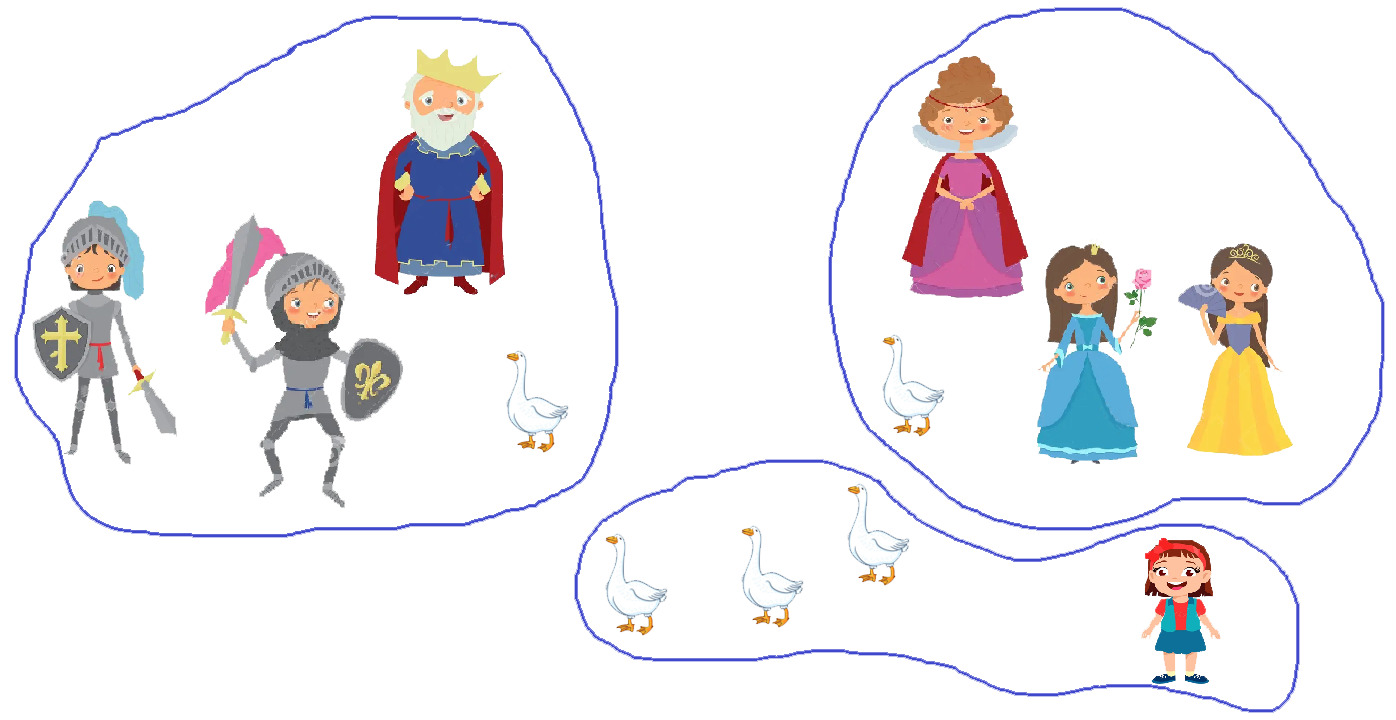
Тя се преструва, че забравя статута си на слугиня, която яде „остатъците“.

Графична или практически ориентирана задача:
- Може да се раздадат фигурки или жетони, които символизират членовете на кралското семейство, гъските и малкото момиче, и чрез тях да се изследват различни варианти на разпределение.

Бележка: Първото разделяне, при което се разпределят главата на краля, врата на кралицата, краката на принцовете и крилата на принцесите, е често срещан мотив в устната литература. Според различни традиции и култури, дялът на майката може да варира, както и обосновката за него: врата – защото „тя носи краля“; сърце или гърди – защото майката е „сърцето на дома“; а понякога дори задната част – защото „всичко се крепи на нея“.