Една кутия има форма и вместимост. Митът започва с поставянето на Хор в саркофаг. Някои кутии са твърде големи, други твърде широки, трети твърде малки. Само кутията, построена специално за Хор, пасва точно. Ето няколко кутии. Как да ги подредите? И по отношение на вместимостта?

Първо ще има прости случаи: една кутия се побира изцяло в друга. После ще има по-сложни случаи: една по-тънка кутия се побира в по-широка, но надвишава по височина. Често учениците се фокусират върху едно измерение и обявяват най-дългата кутия за най-обемна. Необходимо е да се премахне двусмислието чрез пълнене на едната кутия с грис или друг насипен материал и изсипването ѝ в другата. Ако всичко се побира, втората кутия е по-голяма, ако прелива, първата е по-голяма.

С помощта на калкулатор, изчислете $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64}$

Сравнете с $1 - \frac{1}{64}$

На лента хартия, която приемаме за единица, маркирайте чрез прегъване половината, после четвъртина, осмина, шеснадесетина… Визуално разберете, че на всяка стъпка единицата се разлага на :

$1 = \frac{1}{2} + \frac{1}{2} = \frac{1}{2} + \frac{1}{4} + \frac{1}{4} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{8} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{16} = \frac{1}{2} + \frac{1}{4} +$ $\frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{32} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{64}$

Разрежете единичната лента:

След това измерете всяка предложена лента, използвайки само тези малки лентички и запишете резултата.

Подгответе вертикални ленти хартия А4 и техните прости дроби: наблюдавайте, че :

$\frac{3}{4} = \frac{1}{2} + \frac{1}{4} \quad$,$\quad\frac{5}{8} = \frac{1}{2} + \frac{1}{8}\quad$,$\quad\frac{3}{8} = \frac{1}{4} + \frac{1}{8}\quad$,$\quad\frac{1}{3} = \frac{1}{4} + \frac{1}{16} + \frac{1}{64} + \cdots\quad$,$\quad\frac{2}{3} = \frac{1}{2} + \frac{1}{8} + \frac{1}{32} + \cdots$

За последните два случая, използвайте квадрат или равностранен триъгълник, разделяйки на четири малки подобни форми, и повторете вътре. Общата площ се разпределя на три части: червено, синьо, зелено, които от своя страна се състоят от четвъртинки, шеснадесетина, шейсет и четвърта и т.н. Възможност за красиви конструкции и усещане за безкрайност.

Другата версия на парадокса е на Зенон от Елея: Ахил, най-бързият гръцки герой, никога няма да настигне костенурката, защото първо трябва да стигне мястото, където тя е била. Но за това време костенурката ще се е преместила малко, и същият аргумент се прилага. По същия начин стрелата (или бегачът) никога няма да достигне целта, защото трябва да премине половината от пътя. После остава половината от половината, т.е. четвърт, после осмина, шеснадесетина, тридесет и втора, шейсет и четвърта и т.н. Винаги остава разстояние за изминаване.

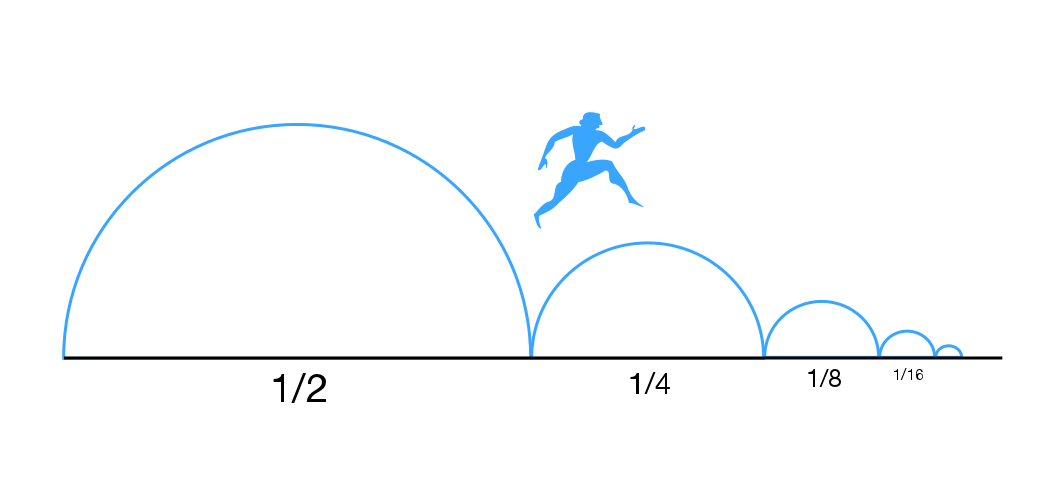
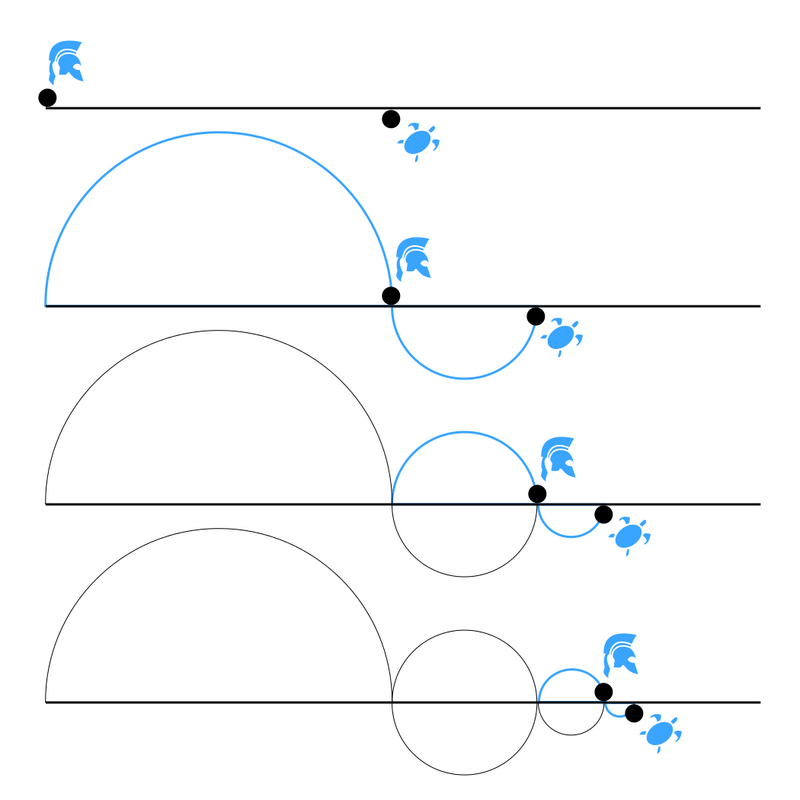
С помощта на калкулатор, изчислете

$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64}$

Сравнете с $1 - \frac{1}{64}$ 

А ако не спираме:

$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{128} + \frac{1}{256} + \frac{1}{512} + \cdots$

А ако делим не на две, а на десет? Какво ще е

$\frac{1}{10} + \frac{1}{100} + \frac{1}{1000} + \frac{1}{10000} + \frac{1}{100000} + \cdots$

Сравнете с $\frac{1}{9}$ 

Тогава какво е $\frac{9}{9} = \,?$  И накрая какво е

$\frac{9}{10} + \frac{9}{100} + \frac{9}{1000} + \frac{9}{10000} + \frac{9}{100000} + \cdots = 0,99999\ldots$

Понятието за граница е усвоено от математиците едва през XIX век. Затова не е изненадващо, че има различни подходи: някои приемат очевидно, че движението е възможно и стрелата достига целта, а други отказват да приемат, че $0,999\ldots = 1$, което от логическа гледна точка е абсолютно вярно. Действително:

$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{128} + \frac{1}{256} + \frac{1}{512} + \cdots = 1$

 което се записва в двоична система като

$1 = 0,11111\ldots_b$

В десетична система (обичайна база), ако

$0,11111\ldots = \frac{1}{9}$

 не създава проблем, както и

$0,33333\ldots = \frac{3}{9} = \frac{1}{3}$

записът

$0,99999\ldots = \frac{9}{9} = 1$

не се приема от учениците. Това е обаче математическо равенство (което се изучава в гимназията, след като се разгледат геометричните редици и техните суми).