Story Summary

A little girl gives a goose to the royal family. Invited to divide it, she symbolically allocates parts of the animal and keeps the largest piece for herself.

Later, she is asked to divide 5 geese among 7 people. Through inventive and clever reasoning, she manages to satisfy everyone…and earns several bags of gold.

About the Story

This tale was popularized in a short form by Leo Tolstoy, especially in his educational texts for children. It draws inspiration from traditional Russian or Eastern wisdom stories, illustrating practical intelligence and cleverness when faced with a difficult task.

The division of geese illustrates:

- an impossible division (5 geese ÷ 7 people),

- a narrative cleverness,

- and the different ways to divide a number into equal parts.

👉 Discover the Story

Maths

Divisions, quotients, distribution…
and an inventive little girl

👦🏻 Target age: 9–11 years (Grades 4–5)
⏰ Estimated duration: 1h
📎 Materials: Tokens (7 red, 5 blue), paper, figurines.
Optional extension: discussions about the remainder in division, sharing games, work on decomposing a number into factors.

🎯 Educational Objectives

• Understand Euclidean division and the role of the remainder.
• Review Euclidean division vocabulary: dividend, divisor, quotient, remainder.
• Identify a logical cleverness in a blocked situation.
• Share a set of objects into subsets of equal cardinality.

🔢 Mathematical Concepts

• Euclidean division: $a = b \times q + r$ (where a is the dividend, b the divisor, q the quotient, r the remainder).

Examples:

$10 \div 6$: Quotient is 1 and remainder is 4; so $10 = 6 \times 1 + 4$

$5 \div 3$: Quotient is 1 and remainder is 2; so $5 = 3 \times 1 + 2$

$5 \div 2$: Quotient is 2 and remainder is 1; so $5 = 2 \times 2 + 1$

Cleverness: The little girl adds the dividend, divisor, and counts herself. She forms groups of 3 or 4 people incorporating the geese. She plays with the ambiguity of division: are we talking about the number of parts or the size of parts? Division can be seen as a partition (splitting a whole and finding the value of one part) or a quotition (grouping into equal parts and finding how many groups).

🟢 Activity 1. Review: vocabulary and practice of Euclidean division

1) Vocabulary review:

- Dividend: the number to be shared
- Divisor: number of parts or people
- Quotient: number of objects per part
- Remainder: what cannot be divided equally

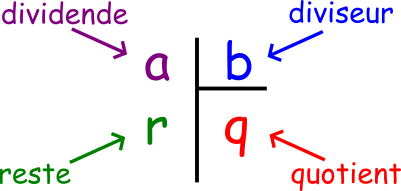
2) Examples to solve:

25 ÷ 4: Quotient 6, remainder 1;

51 ÷ 7: Quotient 7, remainder 2;

10 ÷ 6: Quotient 1, remainder 4;

5 ÷ 2: Quotient 2, remainder 1.

When the remainder is zero, the set can be divided into subsets with the same number of elements. For example, with 15 flowers, we can make 3 bouquets of 5 flowers or 5 bouquets of 3 flowers.

3) Possible ways to divide 12 into equal parts: Use tokens or materials to visualize the parts. We get:

12 = 12 parts of 1

12 = 6 parts of 2

12 = 4 parts of 3

12 = 3 parts of 4

12 = 2 parts of 6

12 = 1 part of 12

🟢 Activity 2. The first “symbolic” division

Reenact the scene with a goose and 7 figurines (king, queen, 2 princes, 2 princesses, the poor girl).
Symbolically associate each part of the goose to a character.

Goal: understand that the division is narrative, not mathematical. The girl places herself outside the calculation, then includes herself at the end.

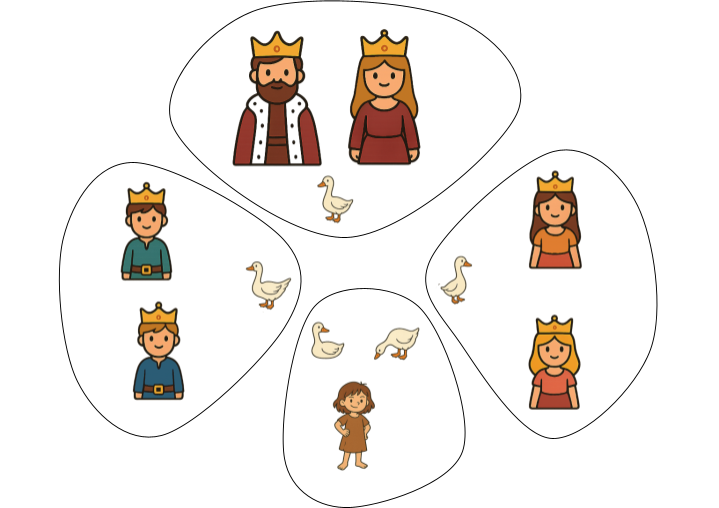
🟢 Activity 3. Division in “3” (in fact: parts of 3)

The girl creates 3 groups of 2 people (king/queen, 2 princes, 2 princesses), excluding herself.

The math division is: 5 ÷ 3, quotient is 1, remainder is 2
→ One goose per group of 2
→ The 2 remaining geese go to the girl, according to her logic: “The poor eat the leftovers of the king’s table.”

From another perspective, she counts the royal family (6 people), the geese (5 geese), and herself; total 12 elements, which she divides into 4 “packs” of 3.

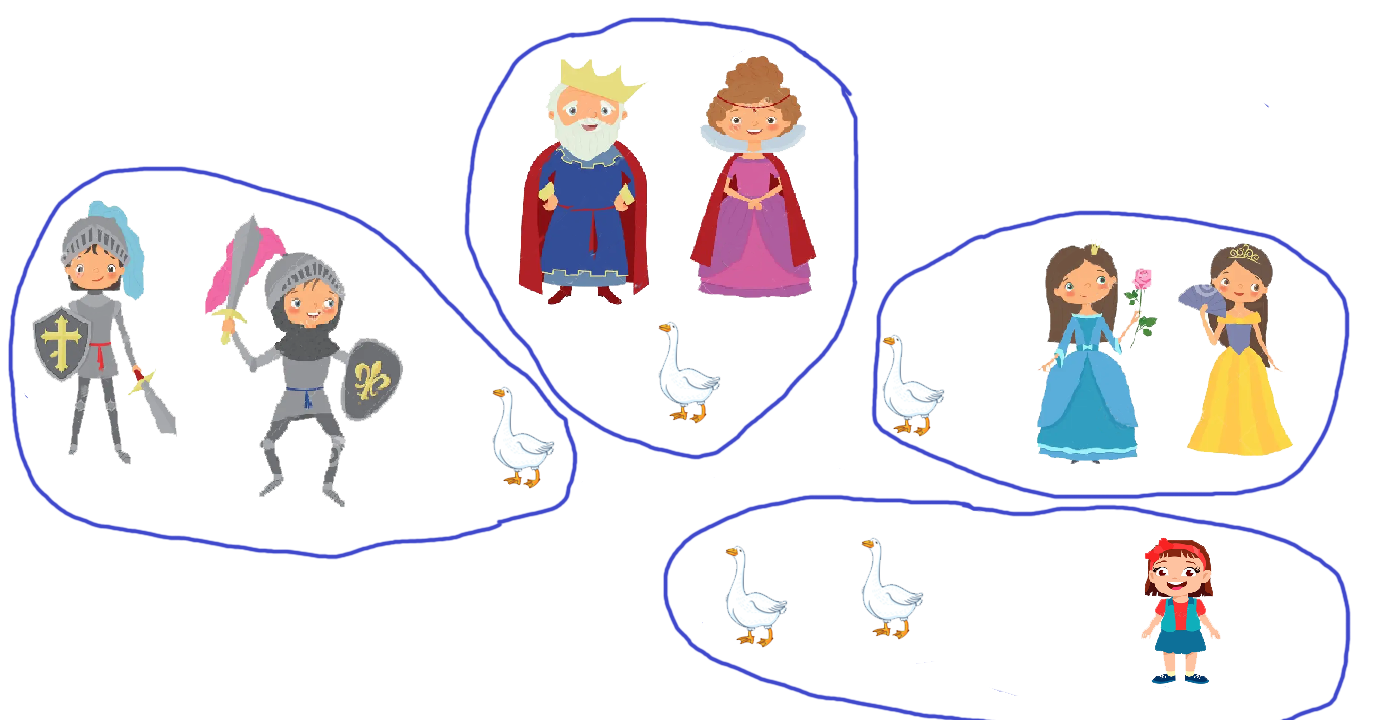
🟢 Activity 3. Division in “4” (in fact: parts of 4)

She first forms two groups of 3 people among the royal family, setting herself aside. If she performed Euclidean division of 5 by 2 (quotient 2, remainder 1), she would give 2 geese to each group of 3 and take one for herself. But this would not follow the “divide into 4” instruction, as 4 does not appear anywhere. Moreover, this division is not advantageous for her.

She thus uses the division: 12 = 3 parts of 4

- (queen, 2 princesses, 1 goose)
- (king, 2 princes, 1 goose)
- (the girl + 3 geese)

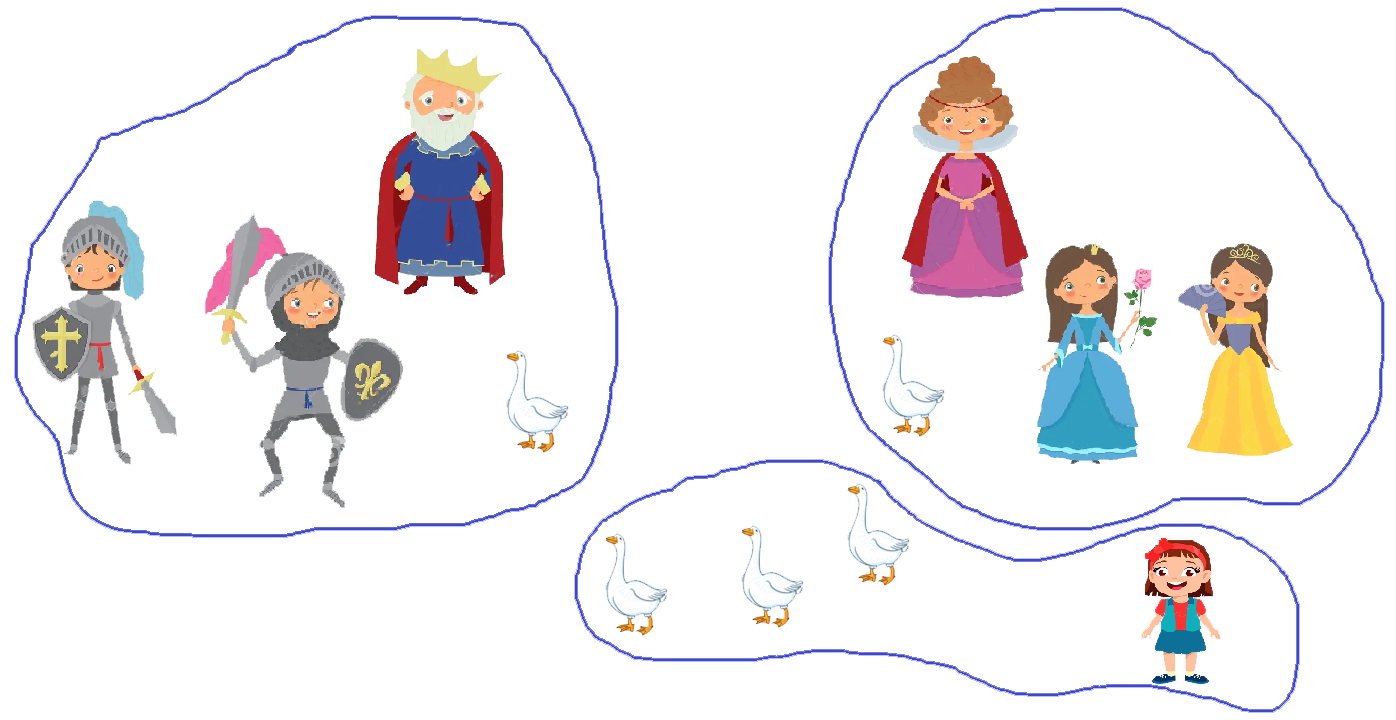
She pretends to forget her status as a servant who eats the “leftovers”.

Graphic or manipulative activity:
- Distribute figurines or tokens representing royal family members, geese, and the girl, and explore the possible distributions.

Note: In the first division, where she gives the head to the king, the neck to the queen, the legs to the princes, and the wings to the princesses, is a common motif in oral literature. Depending on tradition or culture, the mother’s share may vary, as well as its justification: the neck because “she carries the king,” the heart or breast because the mother is “the heart of the home,” or even the rump because “everything rests on her.”