Résumé du conte

Un roi est fait prisonnier après avoir cherché à combattre un monarque cruel. Il demande à sa reine de payer une rançon mais celle-ci préfère passer par la ruse. Travestie en joueur de lyre, elle parvient à libérer son époux, mais ne le met pas au courant du subterfuge. De retour au pays, le roi accuse la reine d'être restée indifférente à son malheur, de l'avoir trahi, jusqu'à ce que les masques tombent et vérité soit levée.

À propos du conte

Ce conte amène le lecteur à entrer dans le point de vue d’un personnage particulier, qui n’a pas toute l’information et qui fait des suppositions. Le roi conjecture et se trompe car les événements surviennent de façon surprenante. Ce récit est un bon point de départ pour aborder les probabilités et la notion d’expérience aléatoire, avec l’idée que l’erreur n’est pas mauvaise, mais fait partie du processus logique.

👉 Découvrir le conte

Maths

Expérience aléatoire, probabilités… et une reine travestie

👦🏻 Âge cible : 9–12 ans (CM1–CM2)

⏰ Durée estimée : 30 min

📎 Matériel : 

🎯 Objectifs pédagogiques

Développer les compétences suivantes :

• Modéliser
• Raisonner
• Planifier

🔢 Notions mathématiques en jeu

• Probabilités (arbre des possibles)

• Logique
• Modélisation

🟢 Activité 1. Lecture interrompue

Étaler la lecture en ménageant des pauses afin de faire établir par les enfants des possibles à différentes étapes:

• Quelles réactions possibles aux razzias du monarque cruel? La coalition aurait pu tenter, plutôt que de l’attaquer, de négocier, proposer une alliance, se protéger; les princes et rois auraient pu envoyer un espion pour avoir des informations ou tenter un assassinat…
• Pendant trois ans, pas de nouvelles. Que peut-il bien se passer?
• Au bout de trois ans, un message. Quel peut-il être? Qui peut l’avoir écrit? Qu’est-ce que ça signifie?
• Quelles réactions possibles de la reine? Vendre tout et proposer une rançon? Pour quelles chances de succès, quel coût, quel risque et quel bénéfice?
• Le roi est effectivement prisonnier, réduit en esclavage depuis 3 ans. Lui aussi s’imagine ce qui se passe dans son pays, ce que fait la reine. Que pense-t-il?
• Un ménestrel arrive, séduit le monarque cruel et repart avec le roi.

Collecter les réponses des enfants sous forme d’un arbre, barrer des branches en fonction des informations données par le conte, invalidant certains embranchements.

🟢 Activité 2. Du hasard, de la connaissance

Le roi ne sait pas ce que fait la reine. Il fait à chaque fois des hypothèses, des paris sur ce qui est en train de se passer. Sans doute aurait-il dû lui faire confiance, plutôt que d’estimer que ce qui lui paraissait évident s’était passé.

Dans une expérience aléatoire, toutes les issues ne sont pas forcément équiprobables. De plus, quand on a certaines informations, les probabilités changent.

Mettez devant les enfants, deux billes rouges et deux billes bleues dans un sac (ou tous autres objets indiscernables au toucher, allant par paires).

Faites choisir les billes tour à tour. Notez les résultats au tableau puis remettez les billes dans le sac. Compilez plusieurs résultats dans une table à quatre colonnes et une dizaine de lignes.

Est-ce que la première bille est plus souvent bleue que rouge (sur votre exemple peut-être, mais si on avait beaucoup de tirages, sans doute pas)? Est-ce que la seconde bille est plus souvent bleue que rouge? La troisième? La quatrième? On dit que les événements “la première bille est rouge” et “la première bille est bleue” sont équiprobables. La chance d’obtenir une bille rouge, que ce soit en première, en seconde, en troisième ou en quatrième position, est à chaque fois d’une chance sur deux. Faire remarquer que le “suspens” n’était jamais très intense pour la quatrième bille, on savait déjà de quelle couleur elle était. De même, quand on sort deux bleues, ce sera immanquablement deux rouges ensuite. Les informations qu’on collecte sur un événement nous permettent d’ajuster nos estimations.

On va étudier seulement la seconde bille, mais maintenant, VOUS prélevez une première bille, que personne ne regarde, que vous mettez directement dans un autre sac.

Il ne reste donc plus que trois billes dans le sac. Posez la question: “et maintenant, la seconde bille, sera-t-elle plutôt rouge, plutôt bleue, ou autant rouge que bleue?”. En fait, on ne peut pas savoir. On fait donc une expérience aléatoire répétée: Faites prélever UNE bille, notez sa couleur et remettez-la dans le sac. Recommencez une dizaine de fois avec des élèves différents.

A priori, vous verrez qu’une couleur sort à peu près 2 fois sur trois, l’autre une seule fois sur trois. Faites alors voter sur la couleur de la première bille contenue dans le sac de la maîtresse. Peut-on le savoir? En est-on sûr? Non, on n’en est pas sûr, on n’a que des soupçons. Vous pouvez organiser plusieurs votes, à chaque tirage d’une seconde bille. Gagne l’élève qui aura le plus de votes corrects, même si les premiers votes sont forcément peu informés.

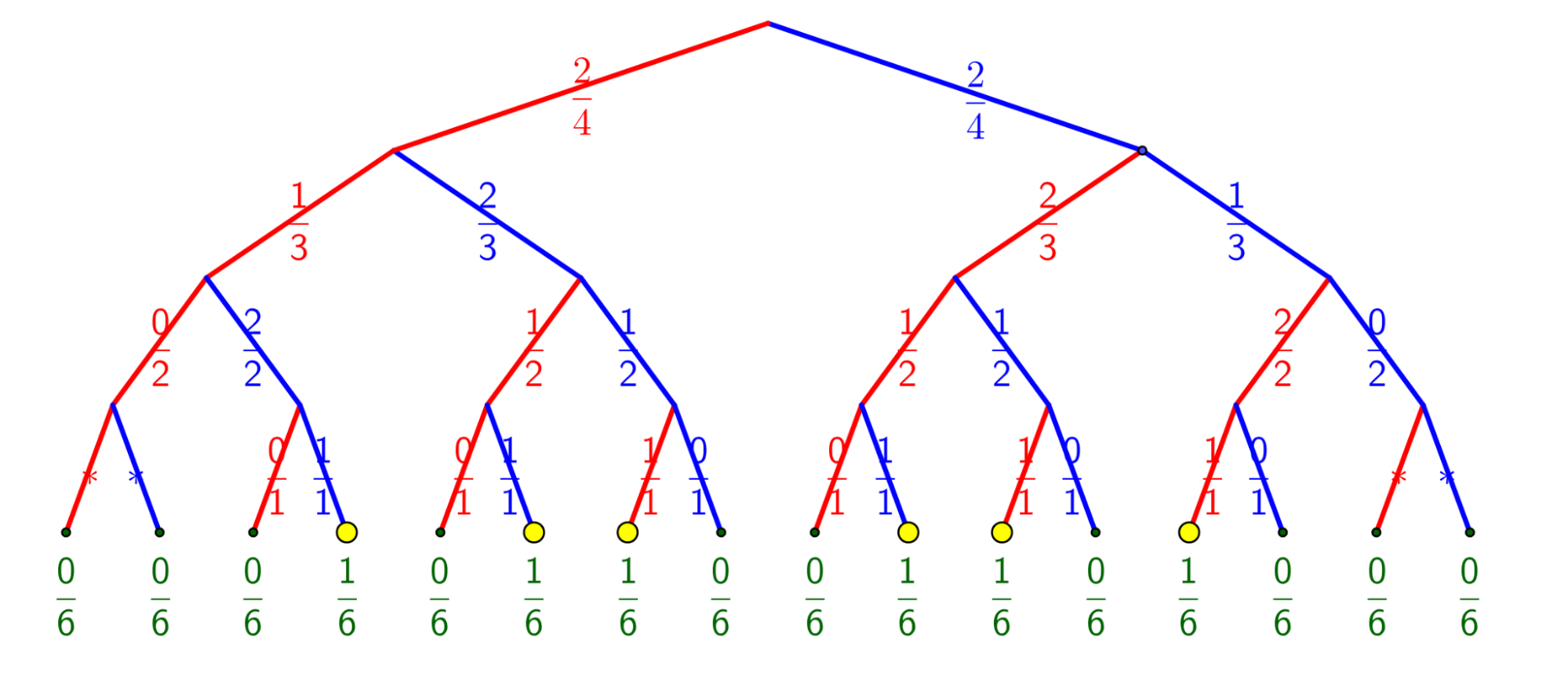
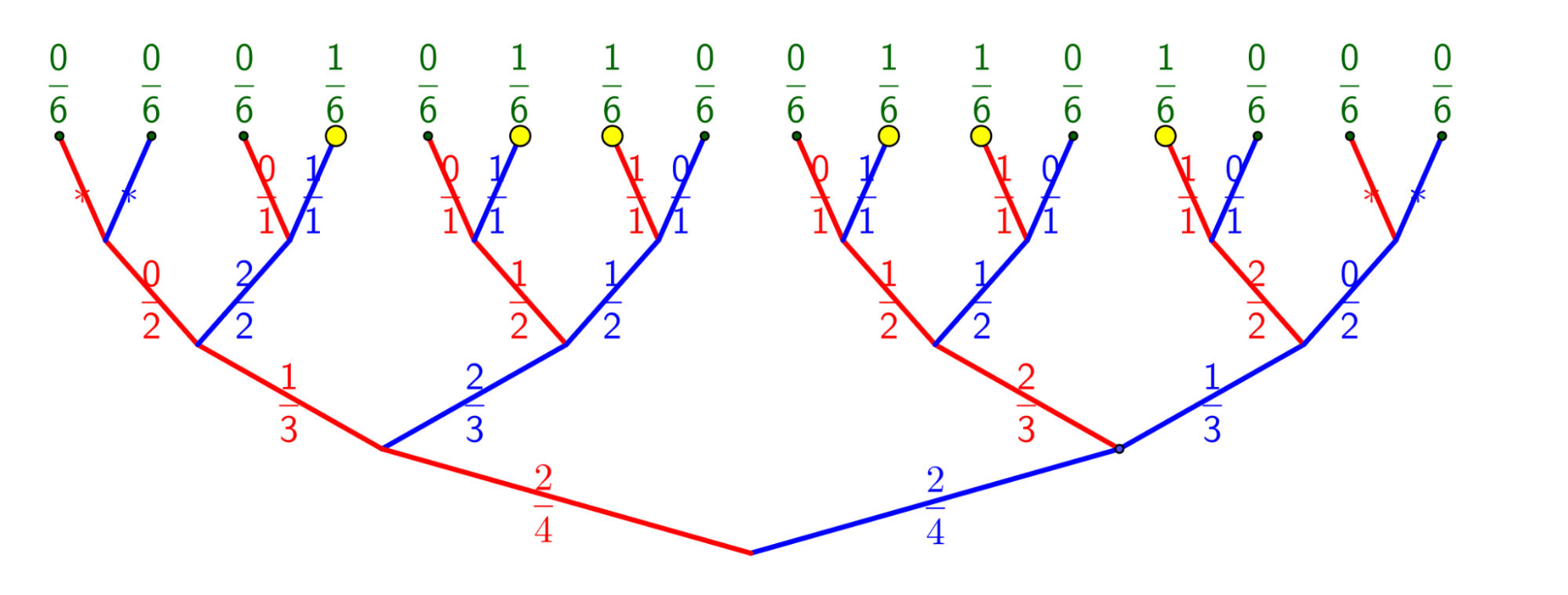
Voici un arbre binaire [choisir vers le haut comme un arbre végétal ou vers le bas comme le sens de lecture des événements et la représentation habituelle en math?] représentant tous les tirages possibles. Et même les impossibles car les seules tirages qui adviennent sont les six qui se terminent par un point jaune, les autres ne respectent pas le nombre de billes de chaque couleur, mais c’est plus pratique de les faire figurer, tout comme on note le nombre 0 quand il n’y a rien. À chaque fois, il y a un choix, et on a marqué sur l’arête le nombre de billes rouges (respectivement bleues) sur le total des billes présentes. À l’étage du haut, il y en a 4, deux de chaque, on a donc 2 chances sur 4 de choisir une rouge et 2 chances sur 4 de choisir une bleue. Ensuite il n’y a plus que trois billes, puis deux, puis qu’une seule (et il n’y a aucun suspens si on connaît les trois précédentes).

On voit que si la maîtresse a pris une bille rouge mais qu’on ne le sait pas encore, alors il y aura deux chances sur trois de prendre une bille bleue au second tirage et une seule chance sur trois de prendre une bille rouge. Mais ça ne dit pas qu’on prendra toujours une bille bleue. C’est ça le hasard.

🟢 Activité 3. Un arbre de Noël fractal

Quand on se pose des questions en cascades, le nombre de cas explose! Pour voir ces nombres qui deviennent de plus en plus grands, voici un découpage adapté pour Noël!

On prend une feuille de papier, orientation paysage, qu’on plie en 2 verticalement. On coupe, du côté de la pliure, depuis le milieu du côté plié jusqu’au centre de la feuille.

On reconnaît dans la feuille 4 quarts. Le quart supérieur de la feuille, du côté de la pliure, on appuie sur sa pliure, ce qui le retourne à l’intérieur, la pliure "montagne" devient une pliure "vallée", qu’on enfonce jusqu’à faire coïncider avec les bords libres de la feuille.

On plie nettement. Un quart de la feuille a disparu. On recommence le processus avec les deux quarts du haut et du bas du côté des pliures (simple pour le quart du bas, double pour celle du haut) : On part du milieu de la pliure jusqu’au centre du rectangle en question, on replie à l’intérieur sa moitiée haute, faisant apparaître de nouveaux plis.

On recommence jusqu’à ce que ce soit trop petit pour les ciseaux… Explications en vidéo.