Mitos
La astucia de Dido
Resumen del cuento
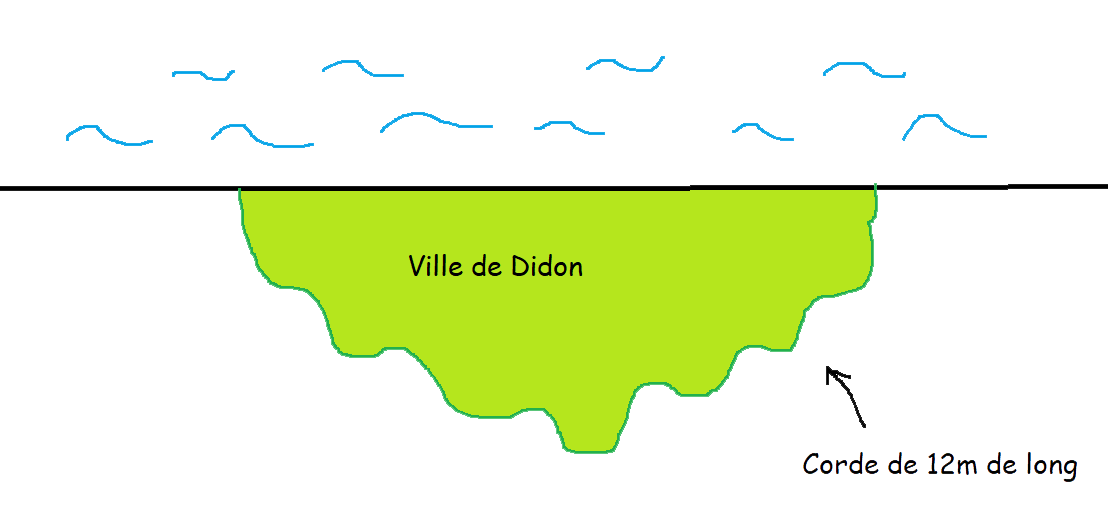
Dido, princesa de Fenicia, huye de su reino tras el asesinato de su marido. Al llegar al norte de África (en Numidia, actual Túnez), negocia con el rey local una condición extraña: recibir tanta tierra como pueda cubrir una piel de toro.
Gracias a un corte ingenioso, convierte esta restricción en ventaja: traza un amplio semicírculo junto al mar, funda la ciudad de Cartago… ¡y le da a la historia una lección de geometría!
Acerca del cuento
Este relato legendario cuenta una fundación de ciudad —pero también una astucia, una negociación y una intuición geométrica sorprendente.
La historia es fácil de contar: sigue una secuencia de acciones claras, con un personaje femenino ingenioso, un reto planteado y una solución sorprendente.
Es un buen punto de partida para hablar de geometría, pero también de lógica y estrategia.
Al alumnado le encanta el giro final: el rey cree haber ganado… ¡pero Dido lo había previsto todo!
👉 Descubrir el cuento
Matemáticas
Perímetros, áreas…
y una reina muy astuta
🔢 Nociones matemáticas en juego
- Cálculo de magnitudes: perímetro, área de superficies habituales (rectángulo, cuadrado, círculo)
- Relación entre perímetro y área
- Propiedades del círculo y del disco
- Modelización
- Uso de fórmulas
- Resolución de problemas.
📋 Prerrequisitos
- Conocer las unidades de longitud y de área (y sus subdivisiones).
- Saber calcular el área y el perímetro de un rectángulo, de un cuadrado y de un círculo (véase anexo).
🟢 Actividad 1. ¡Recorta como Dido!
👦🏻 Edad objetivo: 8–10 años (3.º–5.º de Primaria)
⏰ Duración: 20 min
📎 Material: una hoja A4 por alumno/a o por pareja
🎯 Objetivo
Reproducir el gesto de Dido recortando una hoja A4 en una tira continua para formar un área de forma circular.
🗣️ Consigna para el alumnado
Dido consiguió un gran terreno a partir de una piel de toro. ¿Cómo? Cortándola en una tira muy larga para trazar un círculo. ¿Y si intentamos hacer lo mismo?
Doblad con astucia vuestra hoja para poder recortarla en una sola tira larga. ¡Cuanto más fina sea la tira, más larga será!

💬 Comentarios pedagógicos
Podéis hacer variar varios parámetros:
• El tamaño de la hoja (que representa la piel de toro)
• El ancho de la tira.
Observad lo que cambia:
• ¿Qué ocurre si reducimos el ancho de la banda?
• ¿Qué ocurre si cambiamos el tamaño de la hoja?
• ¿Qué varía y qué permanece constante?
Esta manipulación introduce de forma natural la noción de parámetros.
El alumnado descubre que la longitud de la tira depende de su ancho y de la superficie de partida —y que un perímetro dado delimita un área variable.
🟢 Actividad 2. ¿Qué forma para Cartago? (con rectángulos)
👦🏻 Edad objetivo: 9–10 años (4.º–5.º de Primaria)
⏰ Duración: 30 min
🎯 Objetivo
Encontrar, entre varios rectángulos, la forma que permite construir el área mayor utilizando una cuerda de 12 m. ¡Uno de los lados está bordeado por el mar!
🗣️ Consigna para el alumnado
Dido quería fundar una ciudad usando una piel de toro recortada en tiras. Te toca imaginar la forma ideal para construir Cartago con una cuerda de 12 m. El mar forma uno de los lados del terreno. ¡Adelante!
Ensayo 1: rectángulo de 1 m de ancho
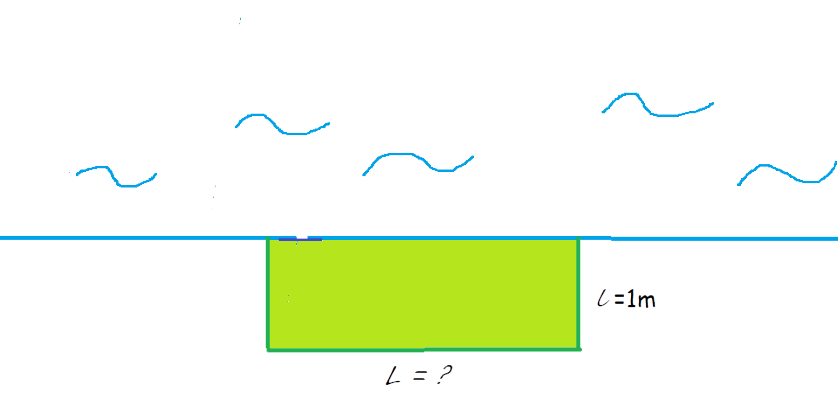
¿Cuál es la longitud L de este rectángulo?
¿Cuál es el área de este rectángulo?
Ensayo 2: rectángulo de 2 m de ancho
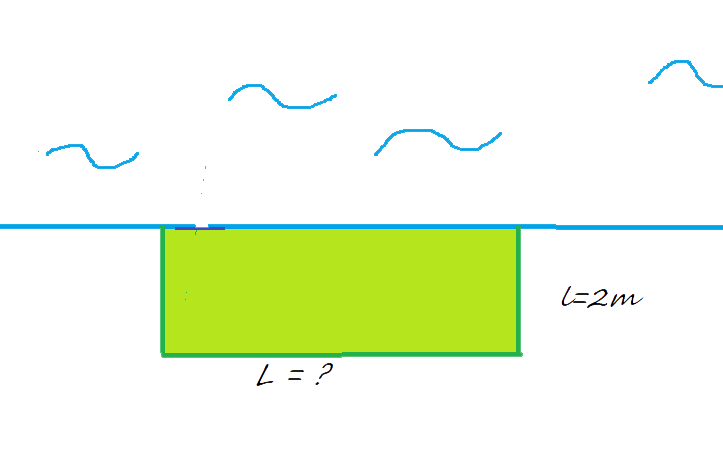
Longitud L = ?
Área = ?
Ensayo 3: rectángulo de 3 m de ancho
Longitud L = ?
Área = ?
Ensayo 4: rectángulo de 4 m de ancho
Longitud L = ?
Área = ?
Ensayo 5: rectángulo de 5 m de ancho
Longitud L = ?
Área = ?
Ensayo 6: con un rectángulo de 6 m de ancho, ¿el área hallada será mayor o menor que la de los rectángulos anteriores?
✅ Conclusión:
¿Qué figura da el área mayor?
Si fueras Dido, ¿qué forma habrías elegido para fundar tu ciudad?
🟢 Actividad 3. El semicírculo de Dido
👦🏻 Edad objetivo: 10–11 años (5.º de Primaria – 1.º de ESO)
⏰ Duración: 30 min
🎯 Objetivo
Con una cuerda de 12 m, realizar una forma que tenga el área más grande posible, sabiendo que uno de los lados estará adyacente al mar. Calcular la superficie obtenida si construimos, como Dido, un semicírculo apoyado en el mar.

🗣️ Consigna para el alumnado
• Con ayuda de la hoja «Anexo», encuentra el radio de este semicírculo.
• Calcula el área del semicírculo.
Conclusión: Con una cuerda de longitud dada, ¿cuál es el mejor diseño para la ciudad de Dido?
🔢 Anexo – fórmulas útiles
Rectángulo
-
Perímetro de un rectángulo:
$P = 2 \times (L + l)$
donde L es la longitud y l el ancho -
Área de un rectángulo:
$A = L \times l$
Círculo
-
Perímetro de un círculo:
$P = 2 \times \pi \times r$ -
Área de un círculo:
$A = \pi \times r^2$
Perímetros, áreas y astucia geométrica
(ficha docente)
Con una cuerda de 12 m, queremos realizar una forma que tenga el área más grande posible, sabiendo que uno de los lados estará adyacente al mar:

Haremos ensayos con rectángulos y cuadrados (actividad 2), y luego con un semicírculo (actividad 3).
🟣 Actividad 2. Rectángulos y cuadrados

Ensayo 1: ancho = 1 m
Calcula la longitud L de este rectángulo. $L = 10\,m$
Calcula el área de este rectángulo. $A = 10\,m^2$
Ensayo 2: ancho = 2 m
Calcula la longitud L de este rectángulo. $L = 8\,m$
Calcula el área de este rectángulo. $A = 16\,m^2$
Ensayo 3: ancho = 3 m
Calcula la longitud L de este rectángulo. $L = 6\,m$
Calcula el área de este rectángulo. $A = 18\,m^2$
Ensayo 4: ancho = 4 m
Calcula la longitud L de este rectángulo. $L = 4\,m$. ¿Qué forma particular tiene? $Cuadrado$
Calcula el área de este rectángulo. $A = 16\,m^2$
Ensayo 5: ancho = 5 m
Calcula la longitud L de este rectángulo. $L = 2\,m$
Calcula el área de este rectángulo. $A = 10\,m^2$
Ensayo 6: ancho = 6 m
Los dos anchos consumen toda la cuerda; no queda nada para la longitud. $A = 0\,m^2$
Ensayo |
Ancho (m) |
Longitud (m) |
Área (m²) |
Observación |
1 |
1 |
10 |
10 |
|
2 |
2 |
8 |
16 |
El área aumenta |
3 |
3 |
6 |
18 |
🔺 Máximo |
4 |
4 |
4 |
16 |
Cuadrado |
5 |
5 |
2 |
10 |
El área disminuye |
6 |
6 |
❌ Imposible (sin cuerda) |
🟣 Actividad 3. Semicírculo
Queremos hallar la superficie obtenida si construimos, como Dido, un semicírculo apoyado en el mar.

- Con ayuda de la parte «Anexo», encuentra el radio de este semicírculo.
$r = \frac{12}{\pi} \approx 3{,}81\,m$
- Calcula la superficie del semidisco.
$A = \frac{1}{2} \pi r^2 = \frac{\pi \times 3{,}81^2}{2} = 22{,}91\,m^2$
✅ Conclusión
Con una cuerda de longitud dada, ¿cuál parece ser el mejor diseño para la ciudad de Dido?
La mejor figura para la ciudad de Dido parece ser el círculo.

