Myths
Петте хляба
Резюме на приказката
Двама мъже споделят хляба си с трети. В знак на благодарност той им дава 5 монети. Но как да ги разделят справедливо, когато единият е дал 2 хляба, а другият 3? Призован е съдия. Вие сте съдията!
Източник: Фибоначи (1170–1250), De duobus hominibus habentibus panes.
Друга, по-стара версия
По-стара версия на този разказ се приписва на Али ибн Аби Талиб, фигура от VII век и познавач на логическите разсъждения. На него се приписва и прочутата загадка за 17-те камили.
В тази версия един човек оставя 8 дирхама на двама други в благодарност за споделена трапеза. А изядените 8 питки са принадлежали неравно: 5 на единия, 3 на другия.
Първият предлага: „Пет дирхама за мен, три за теб.“
Вторият възразява: „Да разделим поравно – по четири и четири!“
Двамата се обръщат към Али, който отсъжда: „Истината, горчива, но справедлива, е че ти имаш право само на един дирхам, а той – на седем.“
За приказката
Този разказ представя математическа загадка в рамките на увлекателна история. Той подканя да се моделира ситуацията, за да се улови справедливото съотношение, и насърчава критичното мислене за разпределението на хлябовете.
👉 Вижте приказката
Maths
Деления, справедливост…
и един „натрапник“!
👦🏻 Целева възраст: 9–10 г. (CM1–CM2)
⏰ Приблизителна продължителност:
📎 Материали: картон в три различни цвята, ножици
🎯 Образователни цели
Развивани математически компетентности:
• Изчисляване
• Моделиране
• Разсъждение
Развивани умения (психосоциални компетентности):
• Търсене на информация
• Критика на предложеното разпределение
• Коригиране
• Аргументация
🔢 Математически понятия включени
• Деление
• Дроби
• Уравнения
• Логика
💬 Педагогически коментар
Какво трябва да направи съдията? За да отсъди, той трябва да разбере какво реално разпределение са осъществили първите двама, при идеята, че всеки е изял еднакво количество хляб!
Решението може да се моделира с фигурата по-долу.
Всеки хляб се разделя на 3 части. Гостът е получил 1 част от първия мъж и 4 части от втория. Може да се каже, че първият е дал само 1 част, а вторият – 4 части.
Следователно справедливото разпределение е 1 монета за първия и 4 монети за втория – противно на първоначалната интуиция и на „непосредствената логика“, че и двамата са дали еднакво.
🧩 Забележка: Едното от решенията не изисква напреднали изчисления. Макар дробите да присъстват неявно, не е необходимо да са изучавани предварително. Историята и дейностите могат да послужат като въведение към тема за дробите.
Всъщност „интуитивните“ решения на двамата не отчитат факта, че всеки е ял – тоест е запазил част за себе си (която не е „инвестирал“ в общото разпределение).

🟢 Дейност 1. Интуицията
По двама или трима ученици в група
🗣️ Инструкция към учениците:
Как според вас двамата мъже могат да постигнат справедливо разпределение, така че всеки от тримата да изяде еднакво количество хляб?
Представете с рисунка тримата мъже, техните 5 хляба и разпределението.
💬 Педагогически коментар
Най-честото (и интуитивно) предложение на учениците е:

– Те естествено раздават по един хляб на всеки.
– Остават два хляба, които разрязват на две и дават по половина на всеки мъж.
– Остава половин хляб, който може да се раздели на 3, за да има по още една част за всеки.
Извод: Разпределението работи на практика, но не е „математически“ отговор в съзнанието на учениците, особено ако дробите още не са изучавани.
🟢 Дейност 2. 15 части за 3 мъже
🗣️ Инструкция към учениците:
Сега разрежете всеки от 5-те хляба на 3 и направете разпределението отново.
💬 Педагогически коментар
Чрез умножение получаваме 15 части, следователно по 5 за всеки.
Напълно естествено двамата мъже вземат своите 5 части от собствените си хлябове.
🟢 Дейност 3. Манипулиране, изрязване
🗣️ Инструкция към учениците:
Изрежете „хлябове“ от картон в два различни цвята (например 3 зелени и 2 сини) и разделете всеки на три части.
🟢 Дейност 4. Към понятието за дроб
Като разделим всеки хляб на 3, имаме 5 пъти по 3 части по $\frac{1}{3}$ хляб, общо 15 части. Може да се запише:
$5 = 5 \times \frac{3}{3} = 15 \times \frac{1}{3} = \frac{15}{3}$
Всеки мъж получава $\frac{5}{3}$ хляба.
Също така:
$\frac{5}{3} = \frac{3}{3} + \frac{2}{3} = 1 + \frac{2}{3}$
🟢 Дейност 5. Разпознаване на равни дроби
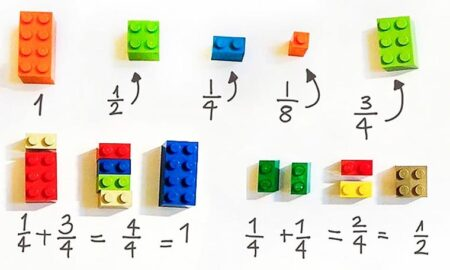
🟢 Дейност 5. А ако са 8 хляба?
Поставете задачата с 8 хляба, при която учениците по-лесно ще стигнат до вярно решение.

