Резюме на приказката

Един цар е пленен след като се опитва да се бори с жесток монарх. Той моли царицата си да плати откуп, но тя предпочита да използва хитрост. Преоблечена като свирач на лира, тя успява да освободи съпруга си, но не му казва за измамата. След завръщането си в страната, царят обвинява царицата, че е останала равнодушна към нещастието му, че го е предала, докато маските не паднат и истината не излезе наяве.

За приказката

Тази приказка насърчава читателите да възприемат гледната точка на герой, който няма пълна информация и прави предположения. Кралят гадае и допуска грешки, докато събитията се развиват по неочакван начин. Историята е добър начин за въвеждане на обсъждане на вероятности и случайни експерименти, като подчертава, че грешките са част от логическото мислене, а не провали..

👉 Открийте приказката

Математика

Случайно изпитание, вероятности... и една маскирана царица

👦🏻 Възрастова група: 9–12 години

⏰ Продължителност: 30 минути

📎 Материали:  

🎯 Педагогически цели

Развиване на следните умения:

• Моделиране
• Логическо мислене
• Планиране

🔢 Математически понятия

• Вероятности (дърво на възможностите)

• Логика
• Моделиране

🟢 Упражнение 1. Прекъснато четене

Спирайте четенето на интервали, за да могат децата да изследват възможни резултати на различни етапи:

• Какви са възможните реакции на грабежите на жестокия монарх? Коалицията би могла да опита, вместо да го атакува, да преговаря, да предложи съюз, да се защити; принцовете и царете биха могли да изпратят шпионин за информация или да опитат убийство...
• Три години без новини. Какво би могло да се случва?
• След три години пристига съобщение. Какво би могло да бъде? Кой би могъл да го е написал? Какво означава?
• Какви са възможните реакции на царицата? Да продаде всичко и да предложи откуп? Какви са шансовете за успех, каква е цената, рискът и ползата?
• Царят наистина е пленен, роб от три години. Той също си представя какво се случва в страната му, какво прави царицата. Какво мисли?
• Пристига странник-музикант, очарова жестокия владетел и си тръгва с царя.

Съберете отговорите на децата в дърво на възможностите, премахвайте клонове според информацията, дадена от приказката, която отхвърля някои разклонения.

🟢 Упражнение 2. Шанс и знание

Царят не знае какво прави царицата. Той прави хипотези, залага на това какво се случва. Вероятно е трябвало да ѝ се довери, вместо да смята, че това, което му се струва очевидно, се е случило.

В едно случайно изпитание не всички резултати са задължително равновероятни. Освен това, когато имаме определена информация, вероятностите се променят.

Сложете пред децата две червени и две сини топчета в чанта (или други неразличими на допир предмети, които са по двойки).

Нека децата изтеглят топчетата наред. Запишете резултатите на дъската, след това върнете топчетата в чантата. Съберете няколко резултата в таблица с четири колони и десет реда.

Въпроси: Първото топче по-често ли е синьо, отколкото червено? Второто? Третото? Четвъртото? Събития като „първото топче е червено“ и „първото топче е синьо“ са с еднаква вероятност. Всеки избор има шанс 50/50. След четвъртия избор вече няма голямо напрежение – цветът може да се отгатне. Наблюдаването на две сини означава, че следващите две трябва да са червени.

Ще изследваме само второто топче, но сега ВИЕ извадете първо топче, което никой да не гледа, и го сложете директно в друга чанта.

Така в първата чанта остават само три топчета. Задайте въпроса: "А сега, второто топче ще бъде по-скоро червено, по-скоро синьо, или еднакво червено и синьо?". Всъщност, не може да се знае. Така че провеждаме повторно случайно изпитание: нека децата извадят ПО ЕДНО топче, запишете цвета му и го върнете в чантата. Повторете десет пъти с различни ученици.

Априори, ще видите, че един цвят излиза приблизително 2 пъти от 3, а другият — само веднъж от 3. Тогава проведете гласуване за цвета на първото топче, което е в чантата на учителката. Може ли да се знае? Сигурни ли сме? Не, не сме сигурни, имаме само подозрения. Можете да организирате няколко гласувания, при всяко изтегляне на второ топче. Печели ученикът, който има най-много правилни гласове, дори първите гласове да са слабо информирани.

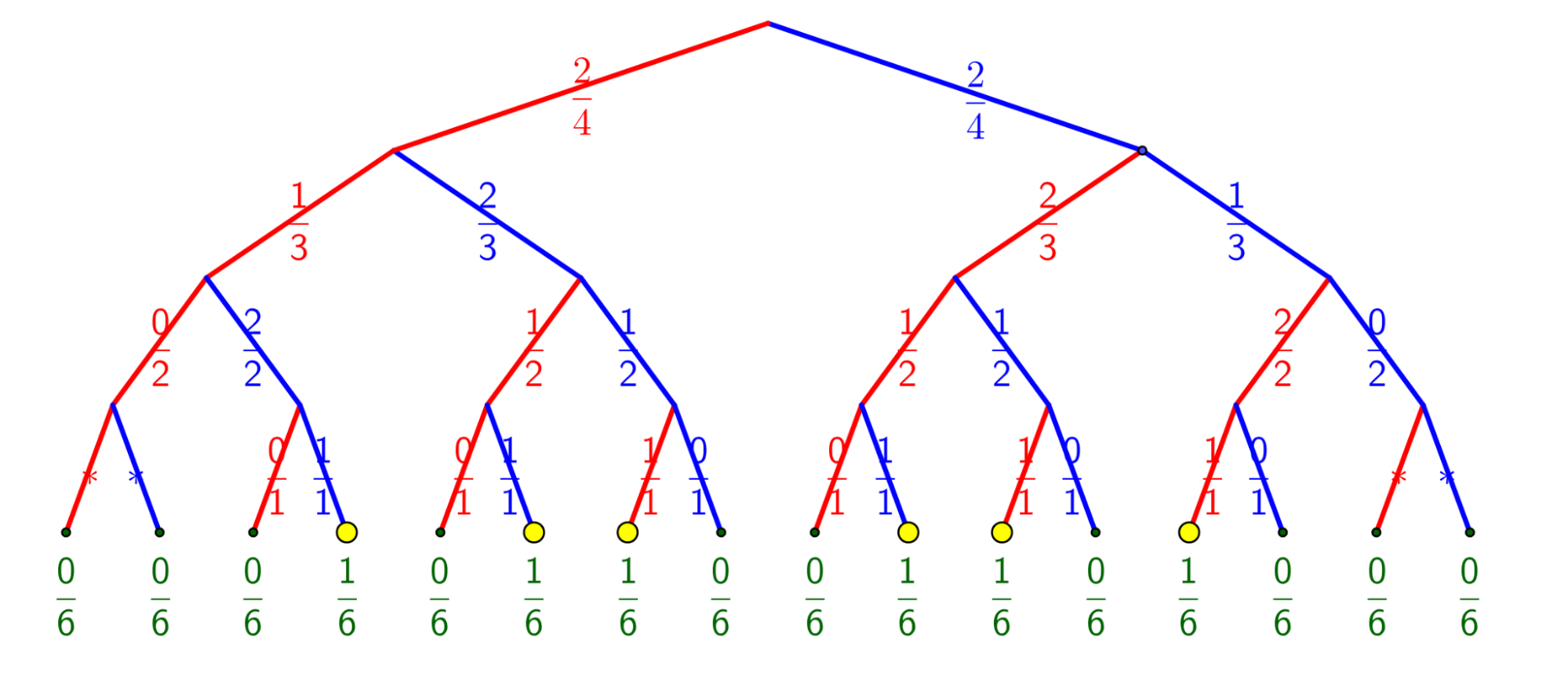
Ето едно бинарно дърво [да се избере нагоре като дърво или надолу като посока на четене на събитията и обичайното представяне в математиката?], което представя всички възможни тегления. Дори и невъзможните, защото единствените тегления, които се случват, са шестте, които завършват с жълта точка, другите не спазват броя на топчетата от всеки цвят, но е по-удобно да ги включим, както отбелязваме числото 0, когато няма нищо. При всяко теглене има избор, и на ръба е отбелязан броят на червените (съответно сините) топчета от общия брой на наличните топчета. На най-горното ниво има 4 топчета, по две от всеки цвят, така че има 2 шанса от 4 да изберем червено и 2 шанса от 4 да изберем синьо. След това остават само три топчета, после две, после само едно (и няма напрежение, ако знаем предходните три).

Вижда се, че ако учителката е извадила червено топче, но ние още не го знаем, тогава при второто теглене ще има две възможности от три да извадим синьо топче и една възможност от три да извадим червено. Но това не означава, че винаги ще извадим синьо топче. Това е случайността.

🟢 Упражнение 3. Коледна елха на възможностите

Когато задаваме въпроси един след друг, възможните отговори стават все повече и повече! Ето една коледна работа с хартия, за да видите как се „разклоняват“ вариантите.

Вземете лист хартия в хоризонтално положение и го сгънете на две по дължина. От сгънатия ръб направете малък разрез от средата към центъра на листа.

Ще видите четири части. Вземете горната част, която е до сгънатия ръб, и я прегънете навътре по вече направената линия на сгъвка. Натиснете така, че сгъвката, която стърчи като „планина“, да се обърне навътре и да стане вдлъбната „долина“, докато горният ръб съвпадне с долния ръб на листа.

Прегънете добре. Една четвърт от листа вече е скрита. Повторете същото с горните и долните части от страната на сгъвките: от средата на всяка сгъвка изрежете навътре и прегънете горната половина навътре, за да се появят нови „клончета“.

Продължете, докато частите станат твърде малки за рязане. Ще получите красива коледна елха с много разклонения. Вижте видео обяснение.