Resumen del cuento

Un rey es hecho prisionero tras intentar combatir a un monarca cruel. Pide a su reina que pague un rescate, pero ella prefiere recurrir a la astucia. Disfrazada de tañedora de lira, logra liberar a su esposo, sin ponerle al tanto del ardid. De vuelta al país, el rey acusa a la reina de haber permanecido indiferente a su desgracia, de haberlo traicionado… hasta que caen las máscaras y la verdad sale a la luz.

Acerca del cuento

Este cuento invita al lector a adoptar el punto de vista de un personaje que no dispone de toda la información y formula suposiciones. El rey conjetura y se equivoca, porque los acontecimientos se encadenan de forma sorprendente. Es un buen punto de partida para abordar las probabilidades y la noción de experimento aleatorio, con la idea de que el error no es “malo”, sino parte del proceso lógico.

👉 Descubrir el cuento

Maths

Experimento aleatorio, probabilidades… y una reina disfrazada

👦🏻 Edad objetivo: 9–12 años (CM1–CM2)

⏰ Duración estimada: 30 min

📎 Material:

🎯 Objetivos pedagógicos

Desarrollar las competencias siguientes:

• Modelizar
• Razonar
• Planificar

🔢 Nociones matemáticas en juego

• Probabilidades (árbol de posibilidades)

• Lógica
• Modelización

🟢 Actividad 1. Lectura interrumpida

Espaciar la lectura introduciendo pausas para que los niños establezcan posibilidades en distintas etapas:

• ¿Qué reacciones posibles ante las razias del monarca cruel? La coalición podría haber intentado, en lugar de atacarlo, negociar, proponer una alianza, protegerse; los príncipes y reyes podrían haber enviado un espía para obtener información o intentar un asesinato…
• Durante tres años, no hay noticias. ¿Qué puede estar ocurriendo?
• Al cabo de tres años llega un mensaje. ¿Qué puede decir? ¿Quién lo ha escrito? ¿Qué significa?
• ¿Qué reacciones posibles de la reina? ¿Venderlo todo y proponer un rescate? ¿Con qué probabilidad de éxito, qué coste, qué riesgo y qué beneficio?
• El rey está efectivamente prisionero, reducido a la esclavitud desde hace 3 años. Él también se imagina lo que pasa en su país y lo que hace la reina. ¿Qué piensa?
• Llega un juglar, seduce al monarca cruel y se marcha con el rey.

Recoger las respuestas de los niños en forma de árbol, tachando ramas según la información que vaya aportando el cuento, invalidando ciertos ramales.

🟢 Actividad 2. Azar y conocimiento

El rey no sabe qué hace la reina. Formula cada vez hipótesis, apuestas sobre lo que está sucediendo. Tal vez debería haber confiado en ella, en lugar de suponer que lo evidente para él había ocurrido.

En un experimento aleatorio, no todos los resultados son necesariamente equiprobables. Además, cuando disponemos de cierta información, las probabilidades cambian.

Pon delante de los niños dos canicas rojas y dos azules en una bolsa (u otros objetos indistinguibles al tacto, por parejas).

Haced elegir las canicas por turnos. Anotad los resultados en la pizarra y devolved las canicas a la bolsa. Compilad varios resultados en una tabla de cuatro columnas y una decena de filas.

¿La primera canica sale más a menudo azul que roja (en vuestro ejemplo quizá sí, pero si hubiera muchos sorteos, probablemente no)? ¿La segunda canica es más a menudo azul que roja? ¿La tercera? ¿La cuarta? Se dice que los eventos “la primera canica es roja” y “la primera canica es azul” son equiprobables. La probabilidad de obtener una canica roja, ya sea en primera, segunda, tercera o cuarta posición, es cada vez de una entre dos. Señalad que el “suspense” nunca era muy intenso para la cuarta canica: ya se sabía de qué color sería. Del mismo modo, cuando salen dos azules, inevitablemente serán dos rojas después. La información que recolectamos sobre un evento nos permite ajustar nuestras estimaciones.

Vamos a estudiar solo la segunda canica, pero ahora, VOSOTROS extraéis una primera canica, que nadie mira, y la ponéis directamente en otra bolsa.

Quedan, por tanto, solo tres canicas en la bolsa. Plantead la cuestión: “y ahora, ¿la segunda canica será más bien roja, más bien azul o tanto roja como azul?”. En realidad, no se puede saber. Por tanto, realizamos un experimento aleatorio repetido: haced extraer UNA canica, anotad su color y devolvedla a la bolsa. Repetid una decena de veces con alumnos distintos.

A priori, veréis que un color sale aproximadamente 2 de cada 3 veces, y el otro 1 de cada 3. Pedid entonces votar sobre el color de la primera canica contenida en la bolsa de la maestra. ¿Se puede saber? ¿Estamos seguros? No, no estamos seguros: solo tenemos sospechas. Podéis organizar varias votaciones, tras cada extracción de una segunda canica. Gana el alumno que obtenga más votos correctos, aunque los primeros votos estén necesariamente poco informados.

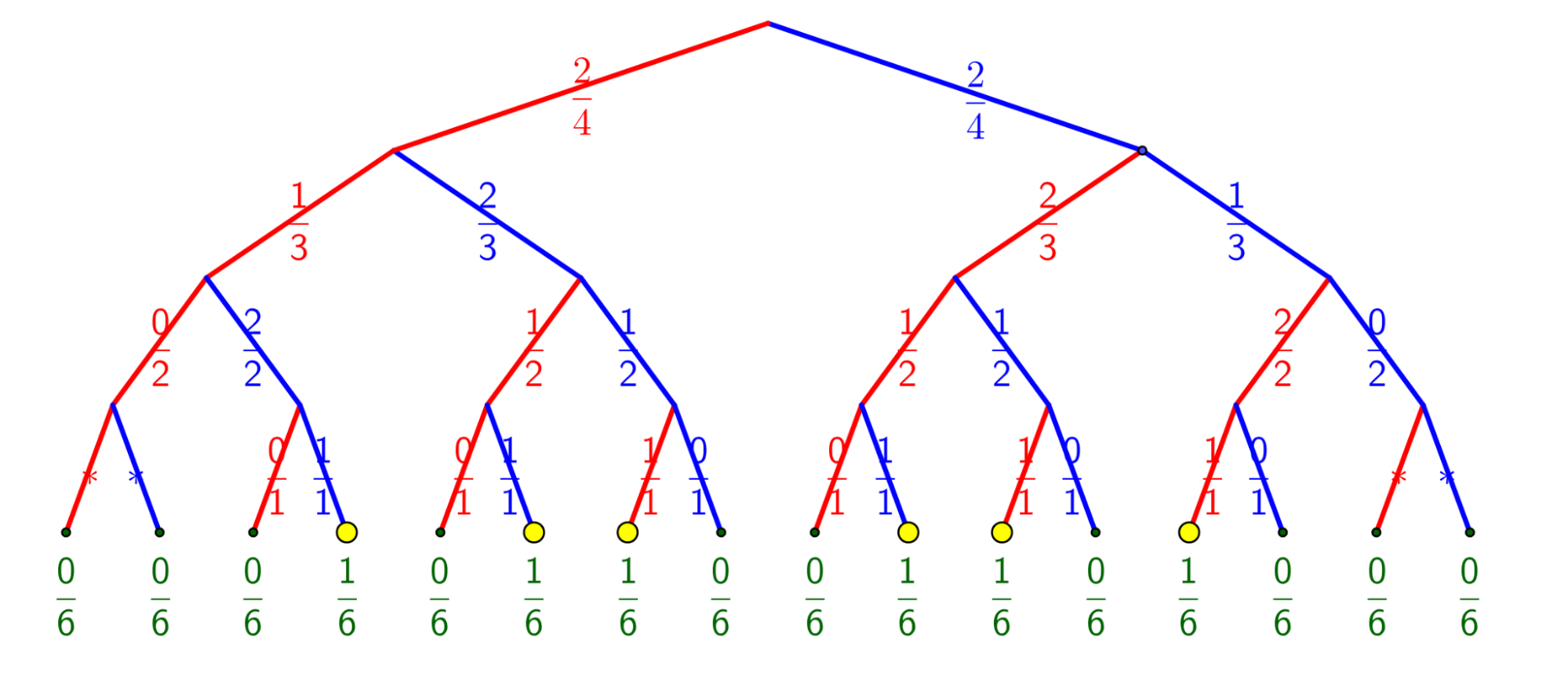
Aquí tenéis un árbol binario [elegir hacia arriba como un árbol vegetal o hacia abajo como el sentido de lectura de los eventos y la representación habitual en matemáticas] que representa todos los sorteos posibles. E incluso los imposibles, pues las únicas extracciones que ocurren son las seis que terminan en un punto amarillo; las demás no respetan el número de canicas de cada color, pero es más práctico hacerlas figurar, del mismo modo que escribimos el número 0 cuando no hay nada. En cada paso hay una elección, y hemos indicado en la arista el número de canicas rojas (respectivamente azules) sobre el total presente. En el nivel superior hay 4, dos de cada color, así que hay 2 posibilidades sobre 4 de escoger una roja y 2 sobre 4 de escoger una azul. Después quedan tres canicas, luego dos, y por último solo una (y no hay ningún suspense si se conocen las tres anteriores).

Se observa que si la maestra ha tomado una canica roja pero aún no lo sabemos, entonces habrá dos posibilidades sobre tres de tomar una canica azul en la segunda extracción y una sola posibilidad sobre tres de tomar una roja. Pero eso no significa que vayamos a tomar siempre una canica azul. Eso es el azar.

🟢 Actividad 3. Un árbol de Navidad fractal

¡Cuando nos hacemos preguntas en cascada, el número de casos se dispara! Para visualizar estos números cada vez mayores, ¡aquí va un recorte adaptado para Navidad!

Cogemos una hoja en orientación apaisada y la doblamos por la mitad verticalmente. Cortamos, por el lado del pliegue, desde la mitad del lado plegado hasta el centro de la hoja.

Reconocemos cuatro cuartos en la hoja. En el cuarto superior del lado del pliegue, marcamos bien el doblez para invertirlo hacia el interior: el pliegue “montaña” se convierte en pliegue “valle”, que hundimos hasta hacerlo coincidir con los bordes libres de la hoja.

Pliegue bien marcado. Ha desaparecido un cuarto de la hoja. Repetimos el proceso con los dos cuartos superior e inferior del lado de los pliegues (simple para el cuarto inferior, doble para el superior): se corta desde la mitad del pliegue hasta el centro del rectángulo en cuestión, se repliega hacia el interior su mitad superior, haciendo aparecer nuevos pliegues.

Se repite hasta que sea demasiado pequeño para las tijeras… Explicaciones en vídeo.