Story Summary

A king is captured after attempting to fight a cruel monarch. He asks his queen to pay a ransom, but she prefers to use cunning. Disguised as a lyre player, she manages to free her husband without revealing the trick to him. Back in the kingdom, the king accuses the queen of remaining indifferent to his suffering and betraying him, until the truth is finally revealed.

About the Story

This tale encourages readers to adopt the perspective of a character who lacks complete information and makes assumptions. The king conjectures and makes mistakes as events unfold in unexpected ways. This story is a good starting point to discuss probabilities and random experiments, highlighting that errors are part of logical reasoning rather than failures.

👉 Discover the Story

🎯 Educational Objectives

• Model
• Reason
• Plan

🔢 Mathematical Concepts

• Probabilities (possibility tree)
• Logic
• Modeling

🟢 Activity 1. Interrupted Reading

Pause the reading at intervals to have children explore possible outcomes at different stages:

• Possible reactions to the cruel monarch’s raids? The coalition might have negotiated, proposed an alliance, protected themselves, sent a spy, or attempted an assassination...
• Three years pass with no news. What might happen?
• After three years, a message arrives. What could it be? Who wrote it? What does it mean?
• Possible reactions of the queen? Sell everything and offer a ransom? What are the chances of success, cost, risk, and benefit?
• The king is indeed imprisoned and enslaved for three years. He imagines what is happening in his kingdom and what the queen is doing. What does he think?
• A minstrel arrives, charms the cruel monarch, and leaves with the king.

Collect children’s responses in a tree diagram, eliminating branches according to story events.

🟢 Activity 2. Chance and Knowledge

The king does not know what the queen is doing. He makes hypotheses and bets on what is happening. In a random experiment, outcomes are not always equally probable. Probabilities change with additional information.

Present children with a bag containing two red balls and two blue balls (or any indistinguishable objects in pairs). Take turns drawing balls, record results, and return them to the bag. Compile several results in a table.

Is the first ball more often blue than red? The second? The third? The fourth? Events like “first ball is red” and “first ball is blue” are equiprobable. Each draw has a 50/50 chance. Note that by the fourth draw, there is no real suspense, as the color can be deduced. Observing two blues means the next two must be reds. The information collected allows adjusting probability estimates.

Now, study only the second ball: draw the first ball secretly, place it aside, leaving three balls. Ask: “What color will the second ball be—red, blue, or equally likely?” Conduct repeated experiments, recording each draw and repeating with different students.

Initially, one color appears roughly twice as often as the other. Let students vote on the hidden ball’s color. Repeat votes after each draw; the student with the most correct guesses wins.

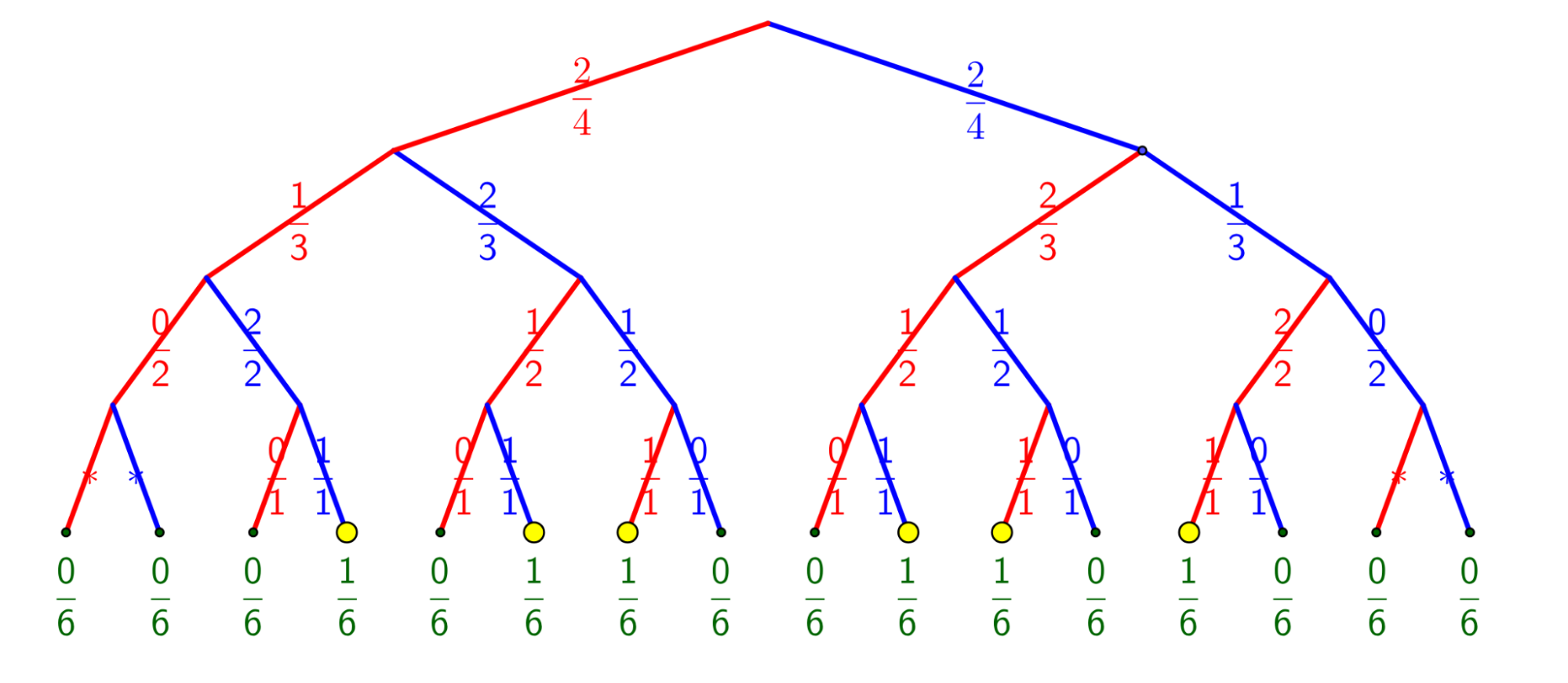
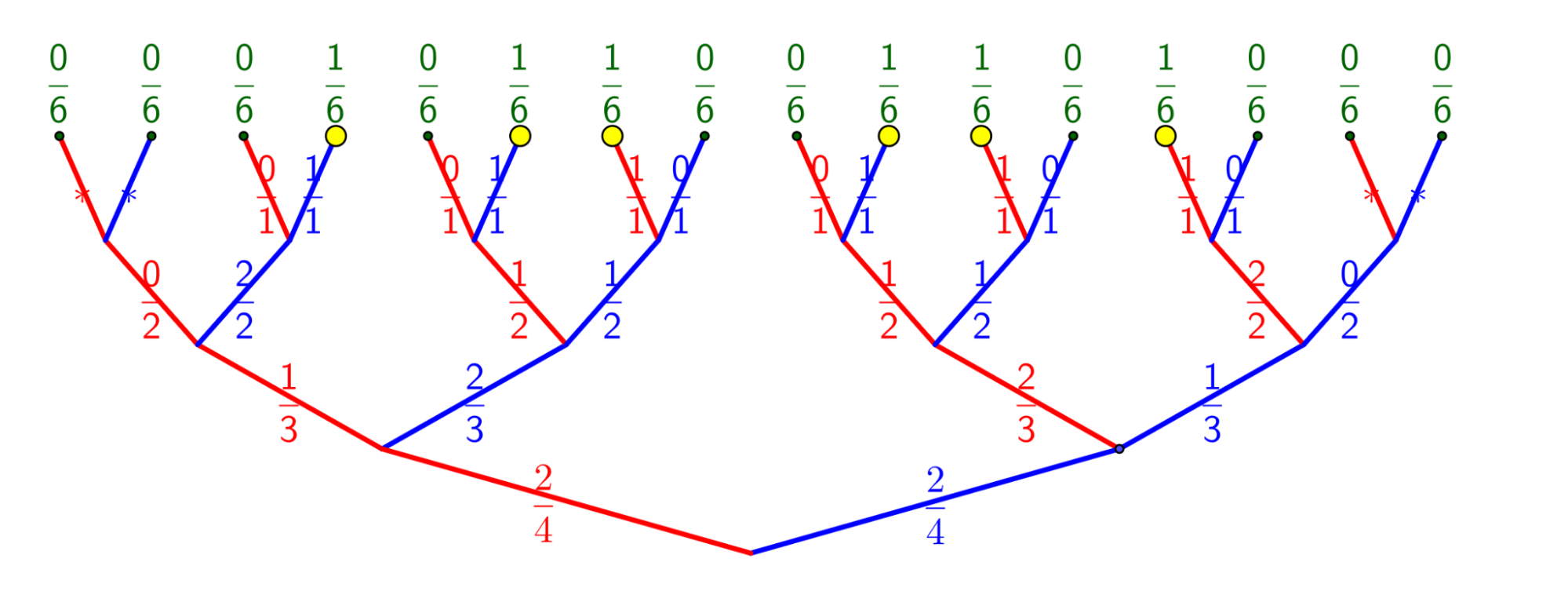
This binary tree [choose top-down like a plant or bottom-up for reading events] shows all possible draws, even impossible ones for clarity. Each branch shows the number of red (or blue) balls out of total remaining balls. At the top, 4 balls (2 red, 2 blue) gives a 2/4 chance for red or blue. Subsequent draws reduce the number of balls. This demonstrates probability in action.

🟢 Activity 3. A Fractal Christmas Tree

Cascade questions quickly increase possible outcomes. Here’s a Christmas-themed way to visualize them!

Take a sheet of paper in landscape orientation, fold in half vertically. Cut from the folded edge’s midpoint toward the center.

You now see four quarters. Fold the upper quarter along its crease so the “mountain” becomes a “valley,” pressing it inside the sheet’s edges.

Repeat for the top and bottom quarters along the folds, creating new folds inside each section.

Continue until the sections are too small to cut. Video explanation here.